算数の合否を分けた一題
青山学院中入試対策・算数の合否を分けた一題（2019年度）
難易度分類
| ［１］ | A |
|---|---|
| ［２］ | Ａ |
| ［３］ | Ａ |
| ［４］ | B |
| ［５］ | B |
| ［６］ | B |
| ［７］ | A |
| ［８］ | B |
| ［９］ | A |
| ［１０］ | B |
| ［１１］ | B |
| ［１２］ | A |
| ［１３］ | (1)B (2)C |
| ［１４］ | (1)A (2)B |
Ａ：青山学院中等部合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して一旦とばした方が良い問題
総評
今年度の問題も、例年通り14問、難易度の傾向も大きな変化は見られませんでした。また、出題単元にも大きく変わった部分はなく、過去問をしっかりと練習してきた生徒にとっては、解きやすかったのではないでしょうか。 ただ、数値の処理や、問題文の文意を掴むのにやや手こずる問題が数問含まれており、そこが、合否を分けた一題になっているのではないかと推察致します。 青山学院中を目指す生徒は、根本原理をしっかりと固めるのはもちろん、難化傾向にある文章題に対応できる応用力を身につけ、取りこぼしのないよう対策をしていきましょう。
問題別寸評
四則演算の基本。
分数・小数の四則演算。積と商の場合は、分数。和と差の場合は小数に直すという基本を忘れずに。
数の推理の問題です。 まずはa×a＝bに注目して、1-9までの整数を当てはめていきましょう。そこまで難しくはないので、飛ばさずしっかりと解き切ってください。
1Lサイズの牛乳パックの重さと、1個牛乳パックをリサイクルすることで、23.4㎏の二酸化炭素を削減できる。
では、68.5千tでは、まずどれだけ二酸化炭素が削減できるかを求めましょう。
さらに、1本の杉が吸収する二酸化炭素の量は14㎏です。
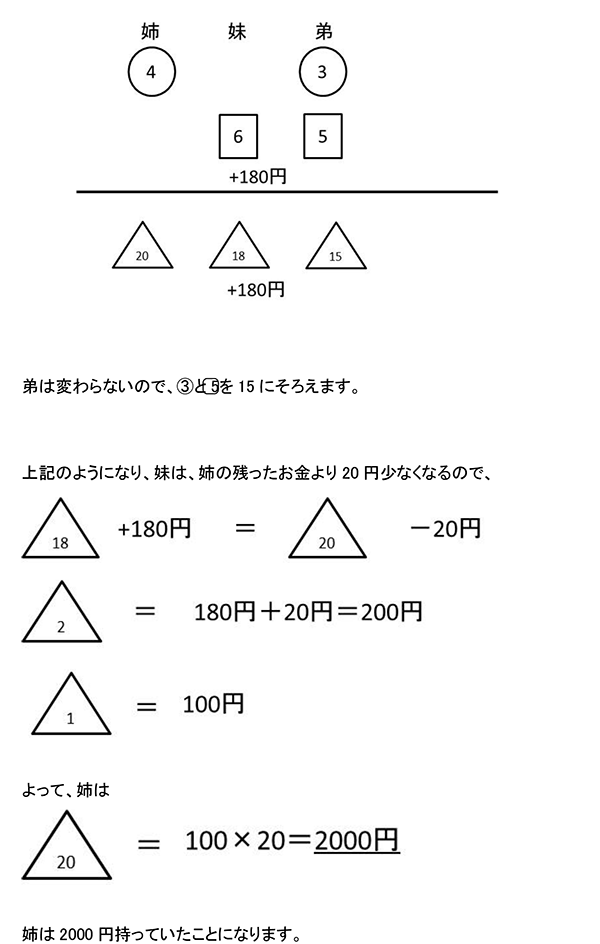
倍数変化、割合、比
問題文より、姉が330円使ってから、弟に400円あげた後の、姉、妹、弟のお金の比を書いていきましょう。
平面図形の面積比の問題。
高さが等しい三角形を見つけ比べていきます。 基本問題となりますのでここは落としてほしくないところです。
連比、逆比
ア、イ、ウの底面積比、高さ比をそれぞれ求めましょう。
先に入館した人たちは、半数以上の人が集まっていたので、先に入った人たちの中の20人は必ず1000円を払っています。
20×1000円＝20000円をまず合計から引いておきます。
63600－20000＝43600円
残りの70-20=50人は、1000円払った人と800円払った人が混ざっているので、
合計43600円、人数の合計50人のつるかめ算になります。
これを見抜けることができたかがポイントです。
50×1000＝50000
50000－43600＝6400
6400÷(1000－800)＝32人
32人+20＝52人・・・これが、先に入館した人数です。
合否を分けた一題で取り上げます。
毎年出ている恒例の、「折ったときの角度」の問題です。
同じ長さの辺には、「チョンチョンマーク」をつけて、正三角形、二等辺三角形を探しましょう。
割合と比の文章題
(1)①②の条件より、
AとBとCの箱の値段の比は、
①②より
A×2＝B×1+C×1
B×2＝C×5
よって、B：C＝⑤：②
A×2＝⑤×1＋②×1＝⑦
A＝⑦÷②＝3.5
A：B：C＝3.5：5：2＝7：10：4
となります。
(2)
Dの箱はCのまんじゅうの個数を5個減らした。
A×2＝D×7より
1箱の値段の比は、A：D＝7：2であり、 A：B：C：D＝7：10：4：2
AとDに入っているお菓子の個数も同じになったとあるので、個数の比を①：①とすると、
1個分の値段の比もA：D＝7÷①：2÷①＝7：2
CとDに入っているものは同じまんじゅうなので、1個分の値段の比は１：１
よって、1箱の値段の比より、入っている個数の比は、
C：D＝4÷1：2÷1＝4：2＝2：1
2‐1＝5個
となり、Dに入っている個数は5個 それが、400円なので、1個は400÷5個＝80円
1箱の値段の比より、 A：B：C：D＝7：10：4：2＝1400円：2000円：800円：400円
Dが5個より、Cは10個
DとAは同じ個数なので、5個
さらに、問題文の条件③より、AとBとCに入っている個数の合計は23個なので、
23－（5＋10）＝8個がB
どらやきは1400円÷5＝280円
もなかは2000円÷8＝250円
まんじゅうは400÷5＝80円
となります。
(1) 合計点20点の人は、第1問、第2問、第3問があっていた人
合計15点の人は、第1問と第2問か、第1問と第3問があっていた人
合計10点の人は、第1問か第2問と第3問があっていた人
合計5点の人は、第2問か第3問があっていた人
となります。
第一問が正解した人が22人いるので、20点と15点の人達が、4人＋13人＝17人なので、
22－17＝5人・・・これが10点取った8人の中に含まれる人数。
よって、10点を取った人の中で、8－5＝3人が第2問と第3問ができた人。
20点の人が4人いるので、第2問と第3問が全体でできた人は、4＋3＝7人となります。
(2)17‐4‐3＝10人・・・これが、15点と5点を取った人の中で第2問ができた人数。
13＋6＝19人・・・第2問か、第3問ができた人
19‐10＝9人・・・これが、第3問を正解した人数
合否を分けた一題
【11】を取り上げます。
平均点の問題ですが、2科目の平均点と表の2か所に穴があるため、人数の合計がわからず、何を使って解けばいいのかが見つけにくい問題となります。
ポイントは、
Aが算数も国語も3点の人数、Bが算数も国語も4点の人数であるということです。
では、まず、
A、B以外の国語の合計点は、1×2+2×5+3×5+4×10+5×11＝122
A、B以外の算数の合計点は、1×3+2×3+3×9+4×8+5×10＝118
国語の合計点＝3.6×□人＝122+A×3点+B×4点
算数の合計点＝3.5×□人＝118+A×3点+B×4点
赤の波線のところが同じなので、
上の式と下の式を引くと、赤の波線部分が消えて、
（3.6-3.5）×□＝4
□＝4÷0.1＝40人 これが、クラス全員の人数です。
ここからは、
国語の合計でも算数の合計でもどちらを使っても出せますが、
今回は、国語の合計を使って、つるかめ算で解いていきましょう。
3.6×40=144点
40-33＝7人・・・AとBの合計人数
144－122＝22点・・・AとBの合計得点
7×4点＝28 28-22＝6 6÷(4-3)=6人・・・これが、3点の人数、A
7-6=1・・・これが、4点の人数、B
答え A＝6人、B＝1人
(1 投票, 平均値/最大値: 3.00 / 5)
Loading ...
青山学院中入試対策・関連記事一覧
青山学院中入試対策・同じ教科（算数）の記事
青山学院中入試対策・同じテーマ（合否を分けた一題）の記事
他校の同じ教科（算数）の記事
