算数の合否を分けた一題
慶應普通部入試対策・算数の合否を分けた一題(2016年度)
難易度分類
| 1 | ①A ②A |
|---|---|
| 2 | B |
| 3 | ①A ②A |
| 4 | ①A ②B |
| 5 | A |
| 6 | B |
| 7 | ①A ②C |
| 8 | ①A ②B |
| 9 | B |
A…慶應義塾普通部を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題
問題別寸評
①
逆算。手順通りやれば解ける問題ですので、普通部の計算の中では平易なものです。
②
工夫が必要な計算。普通部の特性も考えると、順に筆算して解くのではないのは明らかです。結合法則が使える形に直してから計算しましょう。
集合算。まずは問題を読んだとき、または読みながら問題文を表にまとめられたかどうかが大切です。手間を惜しんではいけません。あとはそれぞれの比を記号にして、消去算でどれか一つの記号に揃えてください。
①
ダイヤグラム。太郎君と次郎君のグラフは左右逆転した形になりますが、より確実に答えるためには線分図にまとめるのが良いでしょう。簡単なもので構いません。頭の中で条件をわかったつもりになって間違えてしまうのが一番もったいないです。
②
①でグラフが書けていれば難しくはありません。相似形を利用しましょう。
①
場合の数。赤の旗、青の旗を上げている人数を書き出した後に、誰が何色を上げているのかを考えます。また、「青い旗の本数が赤い旗『より』多くなる」という点にも注意が必要です。
②
①では赤と青の2つでしたが、ここに「両方とも上げない」が加わります。3つの場合でも解法は①と同様です。
推理。入試問題として出題される推理の中では非常に易しいものです。時間をかけず確実に正解したい一題です。
平面図形。受験生なら見覚えはある図形ですが、解法を思い出せたかどうかが所要時間・正答率に大きく影響した問題です。四隅の三角形に各々と同じものをくっつけて長方形を作ると縦4㎝、横3㎝の長方形が重なりになります。また、矛盾がない範囲で適当に長さを決めてしまっても答えは変わらないので、長さを決めて長方形から四隅の三角形を引くのが楽であったかもしれません。
7
①
数の性質。Cを小さくすると、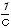 は大きくなることに注意しましょう。引き算の答えを大きくするには、引かれる数は大きく、引く数は小さくします。
は大きくなることに注意しましょう。引き算の答えを大きくするには、引かれる数は大きく、引く数は小さくします。
②
実際に作業してみると、考えられる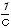 はさほど多くはないことがわかります。しかし、短時間の試験での時間効率を考えると、一度とばしておいた方が良い問題です。焦って考えるよりも、残りの問題を埋めた上で落ち着いて調べていきましょう。合計するときは、各々
はさほど多くはないことがわかります。しかし、短時間の試験での時間効率を考えると、一度とばしておいた方が良い問題です。焦って考えるよりも、残りの問題を埋めた上で落ち着いて調べていきましょう。合計するときは、各々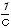 を求めてからではなく、
を求めてからではなく、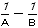 の形のまま計算すると計算がずいぶん楽になります。
の形のまま計算すると計算がずいぶん楽になります。
8
①
平面図形。①、②とも知識が求められる問題です。詳しくは後述しますが、普通部の受験生であれば①はぱっと思いついてほしいレベルです。
②
3点を通る円の中心の位置については知らなかった受験生が多かったのではないでしょうか。中心の位置がわかれば、①の考え方がヒントになります。作問者の誘導にも気付いてほしい問題でした。
9
回転体の体積。試験時間内であっても正確に計算できる力が求められました。少しでも計算の過程を少なくするために、円錐台の体積の導出には体積比も利用できるようになっておきましょう。
合否を分けた一題
最初に慶應義塾普通部の問題構成、特徴について触れておきます。例年8~10個の大問から構成されており、今年の大問は9個でした。大問には小問がついていないものと小問が2つついているものがあり、全体の設問数14問も例年通りと言えます。大問1の計算問題の後には小問集合と呼ばれるものがなく、15問前後の設問を40分でこなせるスピードが求められるのが慶應義塾普通部の特徴です。また、式・解き方を記述させる解答用紙への対策も必要です。限られたスペースに自分の考えを過不足なく書き記す力や、正答に至らなくとも部分点を与えられる答案を書く力は過去問を解き、必要な添削を受けて養われます。
今年の試験は最近の中では易しいものであり、合格するには例年に比べて高い得点が求められたと考えられます。難易度・作業量において試験時間の中で正解することが非常に困難な問題や、知識・経験の有無が結果に大きく影響する問題は例年いくつか見られましたが、今年の試験では非常に少なくなっています。既習の問題を速く正確に処理できた受験生とそうでない受験生の間で、得点に大きく差のついた試験でした。
大問1は例年と同じく計算問題で、工夫して計算することが求められています。過去問を練習できていれば十分対応できるものでした。速さ・場合の数は毎年出題されている分野ですが、年によってその難易度には差があります。今年の試験では速さ・場合の数ともに、これまでの出題と比較すると易しいものであったので是非とも得点源としたい問題でした。図形分野では毎年、平面図形だけでなく立体図形からも出題があり、内容は相似形を利用するものから図形の性質を問うものまで様々です。今年の平面図形(大問7)では知識が問われると同時に、誘導の利用が求められました。立体図形は回転体の体積を求めるものでしたが、慶應義塾普通部合格のためにはこのレベルの問題を確実に正解できる力が欲しいところです。
以下では、上述の大問7を今年の合否を分けた1題として取り上げます。①では合同な直角三角形4つで外側と内側に大小2つの正方形を作ることができるという知識、②ではある2点を通る円の中心はその2点を結ぶ線分の垂直二等分線上にあるという知識、さらに円の半径が求められなくとも①の誘導から半径×半径が求められることに気付く力が問われました。②の誘導にまで気付いた受験生と、①の知識すら持っていない、あるいは思い出せなかったり忘れてしまっていた受験生では、試験中のわずかな時間で大問1つ分の得点差が生じてしまいました。
① 次の図のように辺ABを斜辺とする直角三角形ABEを考え、この直角三角形ABEと合同な直角三角形3つで正方形EFGHと正方形ABIJを作ります。この正方形ABIJが問われている「点Aと点Bを結んだ直線を一辺とする正方形」となります。
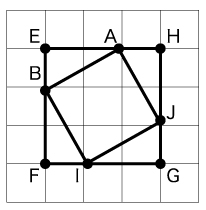
また、正方形ABIJの面積は、
3×3-1×2÷2×4=5(㎝2)
② 2つの点A、Cを通る円の中心は線分ACの垂直二等分線上にあり、同様に2つの点C、 Dを通る円の中心は線分CDの垂直二等分線上にあります。よって、3つの点A、C、Dを通る円の中心は次の図の点Оになり、その半径はOA=OC=ODとなります。
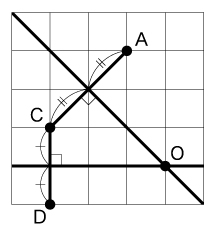
点A、C、Dを通る円の半径の長さを求めることはできないが、半径×半径がわかれば円の面積を求めることができます。ここで①と同様に次の図のようにしてOA(OD)を一辺とする正方形の面積を考えます。
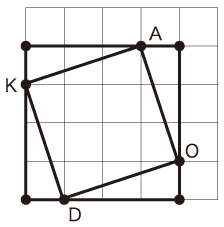
正方形AKDOの面積は、
4×4-1×3÷2×4=10(㎝2)
よって、求める円の面積は、
10×3.14=31.4(㎝2)
慶應普通部入試対策・関連記事一覧
慶應普通部入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 算数の合否を分けた一題(2010年度)
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 塾ごとの算数の学習法の提案(日能研生)
- 算数担当講師から慶応普通部入学を目指す受験生へのアドバイス
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
慶應普通部入試対策・同じテーマ(合否を分けた一題)の記事
- 算数の合否を分けた一題(2010年度)
- 国語の合否を分けた一題(2012年度)
- 社会の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 国語の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)
- 算数の合否を分けた一題(2021年度)
- 国語の合否を分けた一題(2021年度)