算数の合否を分けた一題
慶應中等部入試対策・算数の合否を分けた一題(2019年度)
難易度分類
| [1] | (1) A (2)A (3)A (4)A |
|---|---|
| [2] | (1) A (2)A (3)B (4)A |
| [3] | (1) A (2)A (3)A (4)B |
| [4] | (1) A (2)B |
| [5] | (1) B (2)B |
| [6] | (1) B (2)B |
| [7] | (1) B (2)C |
A:慶應中等部合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C:難度・処理量から判断して、得点差がつかない問題
出題総評
出題傾向、問題数共に、例年通りの形式です。[1]が計算、[2]は一行題、[3]が平面図形・回転体、[4]速さと比、[5]水容積、[6]図形上の点の移動、[7]総当たり戦と場合の数となっております。どれも平易な問題になりますので、ケアレスなくしっかりと得点しておく必要があります。[6]の図形上の点の移動では、(2)がやや解きにくく、[7](2)の調べ上げも、答えを出すまでの時間がかかる問題となっております。[7](2)は最後の問題ですので、この問題に時間をかけるよりは、[7]より前に出てくる問題に戻ってケアレスしていないか、文章を読み間違えていないかをチェックして確実に点数をとる方法をとった方がよいでしょう。また、時間配分の練習もしておきましょう。前半[1]-[5]辺りまでをいかにスピードをつけ、正確に解いていけるかが慶應中等合格へのキーポイントとなります。日頃からの過去問の練習に、時間を図って解くということを導入することにより、スピードと正確性の力をつけていきましょう。また、基本を疎かにせず、なぜそうなるのかを考え、理由づけて解答を出せるかどうかということをチェックし対策を練っていきましょう。
問題別寸評
(1)(2)四則演算の基本。今年度はただ計算するかまたは逆算する問題でしたが、過去には、長い式の中で、同じ数値でまとめる問題や、大きな数の等差数列の和を求める問題(平成21年度【1】(2)3707+3711+3715・・・・+3743)なども出題されています。ただ、ただ、左から右へ計算式を解くのではなく、「同じ数字がないかどうか」「工夫できなか」という視点で問題を見ていくようにしましょう。
(3)3桁の整数をつくる場合の数。
(4)倍数変化算です。年齢の差は一定であることに着目して解いていきましょう。
文章題の構成となります。いずれも基本的なことが問われておりますので、落とさないよう計算ミスに気を付けて、完全解答狙いでいきましょう。
(1)すだれ算を利用し、最大公約数が15であり、条件にあう整数を場合分けして求めていきます。
(2)速さの問題です。時速と分速が混ざって出てきていますので、まずは単位をどちらかに揃えましょう。
(3)1時間に何回60°になるかを考えましょう。2:00と10:00のときは、そもそもその時刻で長針と短針が60°となっているのに注意しましょう。
(4)食塩水の濃度を求める基本的な問題です。
図形・立体問題のセットになります。
(1)平行線ときたら、①錯角 ②相似 ③等積変形を思い出しましょう。
平行四辺形の中には相似形が存在します。三角形AEHと三角形CFHは相似です。
EH:HF=3:2より、AE:CF=3:2となるので、AH:HCも3:2となり、
三角形ABHと三角形CGHも相似形なので、AB:GC=3:2
よって、DG=③-②=①が5cmにあたるので、AB=③=3×5=15cmとなります。
(2)二等辺三角形がたくさんあります。外角はとなりにない2つの角度の和ですので、
わかる角度をどんどん記号で表していきましょう。
(3)図形の移動。「点で見るようにする」ことがポイントです。つまり、点Aはどこに動いたのか、点Oはどこまで動いたのか、それをまずチェックしましょう。また、円の半径がわからないときは、「半径×半径」さえわかればよいので、半径BAを□とすると、
□×□÷2=8×8
□×□=64×2=128
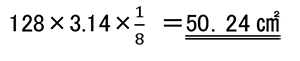
(4)回転体の問題です。表面積を求める問題ですので、部分図を描くようにしましょう。
また、3.14が多く出てきますので、必ず3.14はまとめて、最後に1回だけ計算するように心がけましょう。
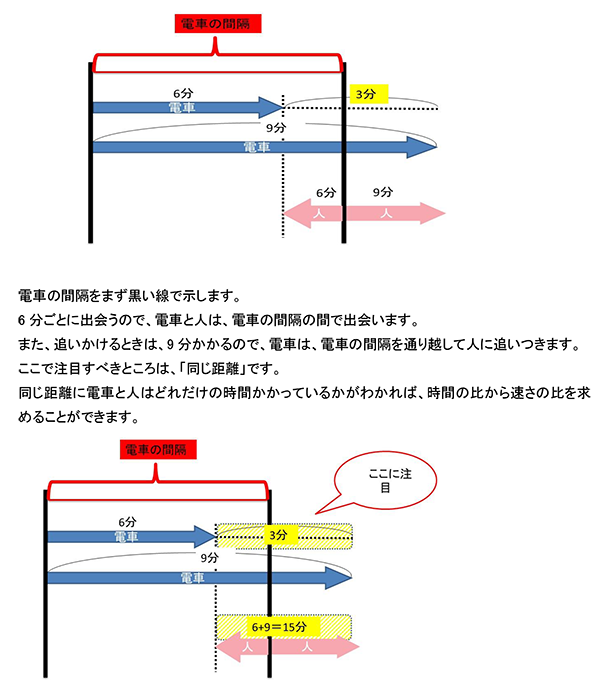
電車と人の出会い、追いかけ、比の利用の問題です。
(1)
電車が3分かかるところを、人は6+9=15分かかります。
時間の比→電車:人=3:15=1:5
速さの比→電車:人=5:1
となります。ということから、人は時速4kmなので、電車の速さは、4×5=20km/時
となります。
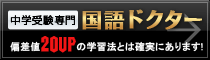
(2)下図を描いてみると、注目すべき点が見えてきます。
速さの問題では、状況をつかむ進行図が有効です。
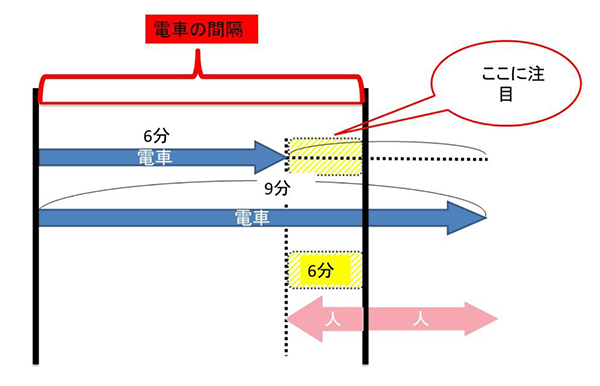
(2)は、人が6分で進んだ距離を電車は何分かかるかを(1)の比を利用して解きましょう。
同じ距離である場合、時間の比は、電車:人=①:⑤でした。
よって、人は⑤に6分かかっているので、電車は6÷⑤=1.2分・・・①
ということは、電車の間隔は、6+1.2=7.2分です。 7分12秒
図形上の2点が動く問題です。
グラフを読み取り、点Pと点Qの速さをまず求めましょう。
(1)8秒後、点Qが先に点Cへ着くので、点Qの速さは48÷8=6cm/秒
また、点Pは48cmに12秒かかったということが読み取れるので、48÷12=4cm/秒
四角形ABQPの面積が、長方形ABCDの面積の半分になるのは、点Pと点Qを結んだ線が長方形ABCDの対角線になるときなので、48×3÷(6+4)=14.4秒後
正方形となるのは、48cmが6個分になるときなので、
48×6÷(6+4)=28.8秒後
(1)勝ち点の場合分けをすると、
(勝ち、引き分け、負け)の順番で回数を書いていきます。
例えば、(2,1,0)→勝ちが2回、引き分け1回、負けが0回で、勝ち点は、2回×3点+1回×1点=7点となります。
このように、全部の勝ち点を書き出すと、
(2,1,0)→7点
(2,0,1)→6点
(1,2,0)→1×3+1×2=5点
(1,0,2)→3点
(0,1,2)→1点
(0,2,1)→2点
(1,1,1)→4点
(3,0,0)→9点
(0,3,0)→3点
(0,0,3)→0点
よって、2位のチームの勝ち点は、最大で、7点、最小で2点です。
(2)(1)より考えられる各チームの勝ち点は、
0,1,2,3,4,5,6,7,9点の9通りです。
全体の試合数は、6試合あり、6回勝ち試合があり、6回負け試合があります。試合の勝ち負けあいこの総数は12回となります。
引き分けを考えると、引き分けは、0回の場合と、2回、4回、6回の偶数回しかないので(2つのチームが引き分けとなるため)
試合総数を表すと、例えば、2回引き分けがあると、
勝ち試合が5試合、引き分け2回、負け試合が5回
この順番で(5,2,5)と書くこととします。
(6,0,6)の時は、勝ち点の合計は、6×3=18点
(5,2,5)では5×3+2×1=17点
(4,4,4)では4×3+4×1=16点
(3,6,3)では3×3+6×1=15点
(2,8,2)では2×3+8×1=14点
(1,10,1)では1×3+10×1=13点
(0,12,0)では12×1=12点
それぞれ、各チームがどのような点数を取っているのか場合分けをしていきます。
18点になるときは4通り
17点になるときは9通り
16点になるときは11通り
15点になるときは10通り
14点になるときは4通り
13点になるときは1通り
12点になるときは1通り
の組み合わせがあるので、全部足すと、4+9+11+10+4+1+1=40通り
合否を分けた一題
[5]を取り上げます。
水量と立体図形の典型問題ではありますが、どの解法を選択するかでかかる時間に差が生じてきます。 実際の体積を求める解法ではなく、比を利用して解くことにより、計算時間の短縮を図り、よりスピィーディーで正確に解ききることを意識しましょう。
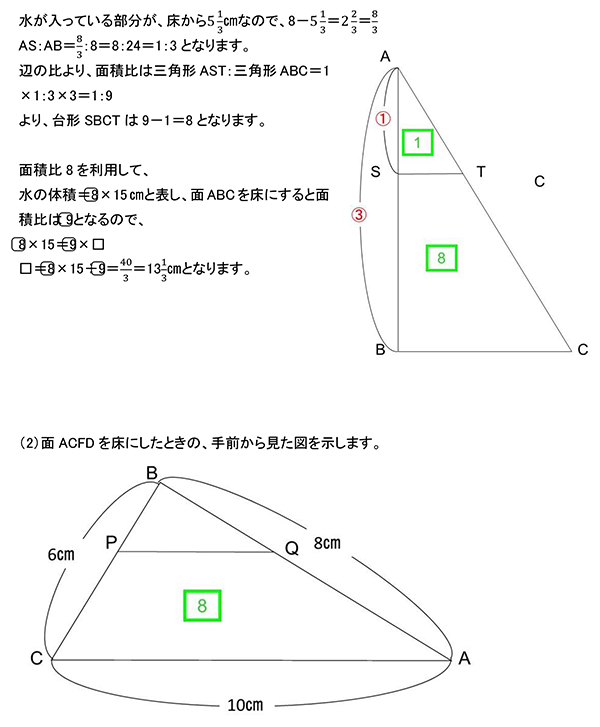
(1)相似形を見つけ、相似比、面積比を利用して解いていきましょう。

慶應中等部入試対策・関連記事一覧
慶應中等部入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 算数の合否を分けた一題(2011年度)
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(日能研生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 算数担当講師から慶應中等部入学を目指す受験生へのアドバイス
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2014年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
慶應中等部入試対策・同じテーマ(合否を分けた一題)の記事
- 理科の合否を分けた一題(2010年度)
- 算数の合否を分けた一題(2011年度)
- 国語の合否を分けた一題(2011年度)
- 社会の合否を分けた一題(2011年度)
- 国語の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2011年度)
- 算数の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2013年度)
- 理科の合否を分けた一題(2013年度)
- 社会の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2015年度)
- 社会の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)
- 国語の合否を分けた一題(2021年度)