算数の合否を分けた一題（2020年度）

算数の合否を分けた一題

早大学院入試対策・算数の合否を分けた一題（2020年度）

難易度分類

大問1	（１）A　（２）B　（３）Ａ　（４）①A　②A
大問2	（１）A　（２）A　（３）B　（４）B
大問3	（１）①A　②A　③B　（２）B　（３）C
大問4	（１）A　（２）B　（３）B　（４）C

A・・・早稲田学院中学部合格を目指すなら、確実に正解したい問題
B・・・知識、解法次第で、得点に大きく差がつく問題　⇒　合否を分けた問題
C・・・難易度、処理量から判断して、正解できなくても合否に影響しない問題

問題別寸評

大問1　小問集合

（１）分数の計算

全ての分数の分母を19×21の形にして後は分配法則を使って解きましょう。
簡単な計算問題ではないですが、なんとか正解したいところです。

（２）分数の計算、約束記号

（１）に約束記号が加わり、計算も少し複雑になったものです。
この問題も（１）同様、分母をそろえましょう。

（３）場合の数

5枚を区別のない2袋に分けるので、分け方は（1個、4個）と（2個、3個）のみです。
それぞれ、5通り、10通りなので、15通りと求められます。
この問題は確実に正解しましょう。

（４）平面図形の折り返し

①問題文より、状況整理していくと下の図のようになるので、AD：BC＝2：5と求められます。

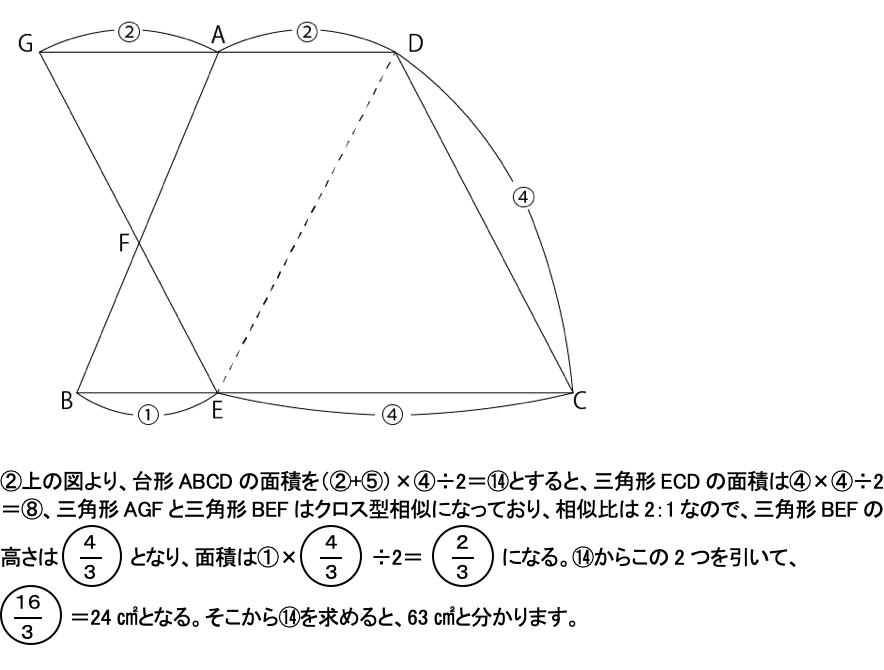
②

大問2

合否を分けた一題として後述します。

大問3　条件整理

入試においてはあまり見られない形式の問題です。
（１）の①、②はほぼ全員正解でしょう。ただ、その後で手が止まってしまった受験生も多いのではないでしょうか。
（１）③問題文から分かることを整理すると下の図のようになります。

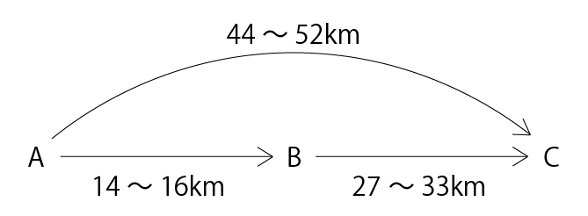
①で求めた、A→Cと②で求めたA→B、B→Cの両方の条件を満たすのは、両方の範囲内に入るときです。
①の範囲は44～52km、②の範囲は41～49kmです。両方に当てはまるのは44～49kmなので、最小の値が44km、最大の値が49kmになります。
（２）（３）も（１）③と同じように考えていきましょう。ただ、（２）、（３）の順に複雑になっていくので、丁寧に求めましょう。

大問４　平面図形、速さ

（１）はシンプルに直径10㎝の半円の長さです。
点Aがどのように動くかイメージできていれば、一瞬で解けたでしょう。

（２）からは少し複雑になります。
もちろん、そのままでも解けますが、正面から見た図を作図すると分かりやすくなります。
下図は高さが2.5㎝のところで左側の三角形の点Aと右側の三角形の点Dがぶつかったときの様子です。

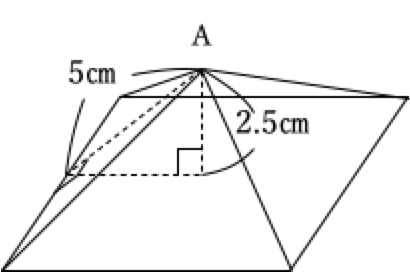
このとき、三角形ABFは下の図より正方形BCEFから30°のところまで動いていることが分かります。

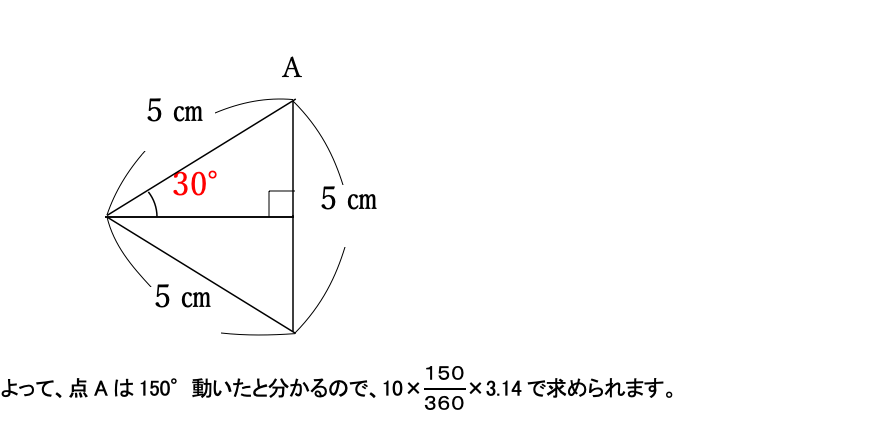
（３）1秒ごとの状況図を描いてみれば、初めて接触する時間が分かります。

（４）左側の三角形は1往復4秒のままで、右側だけ1往復の速さが変わる問題です。
問題文より、16秒以内に左右の三角形が同時に再び折る前の状態に戻ることが1回だけあり、左側の三角形は右側の三角形より速く動くので、右側の三角形は16の約数で4より大きい8秒周期か、16秒周期だと分かります。それぞれ試すとどちらが右側の三角形の1往復する速さが分かります。

合否を分けた一題

この問題は解法さえ知っていれば、（３）（４）を一瞬で解けます。そのため、解法を知っているか知らないかで大きく差がついた問題となります。よって合否を分けた一題とさせていただきました。

大問2　数に関する問題

この問題は、図を描きながら考えてもいいですが、ユークリッドの互除法の知識があれば一瞬で解くことができます。ユークリッドの互除法とは、ある2数の最大公約数を求めるときに使う方法です。この問題では、2つの辺の長さが同じになる長さを求めていくため、2つの辺の長さの最大公約数を探すと、いうことと同じ意味ですので、使っていきます。
ユークリッドの互除法では、2数のうち大きい数を小さい数で割ります。そして、出てきた答えを小さい方の数で割ります。それをくり返していき、割り切れたらそれが2数の最大公約数となります。
（１）は長い辺と短い辺の長さが同じなので、0です。

（２）は、ユークリッドの互除法で解いていくと、
36÷20＝1・・・16
20÷16＝1・・・4
16÷4＝4
となります。この問題では紙を切った回数を求めます。
2回切ると、あとは残りを4等分するので、合計5回切ると分かります。

（３）（２）同様、ユークリッドの互除法で解いていきます。
625÷169＝3・・・118
169÷118＝1・・・51
118÷51＝2・・・16
51÷16＝3・・・3
16÷3＝5・・・1
3÷1＝3
となります。この問題では2数の最大公約数を求めるので、答えは1となります。

（４）この問題では2数の最大公約数と割った回数が分かっているので、ユークリッドの互除法を逆から考えていきます。また、問題文に長い辺が最も短い長方形とあるので、最後は綺麗に2つに切れたと分かります。
すると、一番最後は、□÷7＝2となり、□は14です。
その1つ前は、△÷14＝1・・・7となり、△は21です。
その1つ前は、〇÷21＝1・・・14となり、〇は35です。
よって、答えは35㎝と分かります。

総評

今年度の入試は大問数、小問数ともに例年通りの範疇でしょう。
早稲田高等学院中学部は2015～2017年は実質倍率2.6倍程度でしたが、2018年～2020年は実質倍率3.2倍程度に上がっています。
合格最低点は公表されていませんが、より厳しい戦いになっていると予想されます。
全18問中9問は難易度Aの問題ですので、最低限これらの問題は取りこぼしのないようにしていきたいところです。

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？