算数の合否を分けた一題（2019年度）

算数の合否を分けた一題

浦和明の星中入試対策・算数の合否を分けた一題（2019年度）

難易度分類

［１］	(1)　A　　(2)B　　(3)A　　(4)A (5)B (6)B (7)B
［２］	(1)　A　　(2)A
［３］	(1)　アA　イA (2)ウB　　エB　　(3)　オB　　カA
［４］	(1)　A　　(2)B
［５］	アA　　イA　　ウA　　エA　　オB

Ａ：浦和明の星合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難度・処理量から判断して、得点差がつかない問題

総評

出題傾向、問題数共に、例年通りの形式でした。［1］は、計算と一行題の小問集合。　［2］は、水量とグラフ。［3］が規則性、［4］速さと比、［5］立体の表面積と規則性が絡んだ問題となっておりました。特にいわゆる難問は無いので、計算ミスなく得点しておく必要があります。
基本問題でどのような根本原理を使っているのかを日ごろから意識しながら練習し、応用問題では、根本原理に気づけるようになることが大事です。ただただ、式や解き方を暗記するのではなく、どういう考え方を利用しているのか、浦和明の星女子中の過去問を使いながら、練習することをお勧めいたします。［1］でも、レベル別でBにした問題（2）、（5）、（6）、（7）は、特に、解き方がすぐわかるというよりは、どうなっているのかを自分で考えてから解き進める必要があります。正五角形の性質、円の性質、植木算・・・など、言葉は聞いたことがあり、言えば理解はできると思うのですが、その基本性質をどうやって使うか、どの部分に使うかということを自分で判断しなくてはいけません。日ごろから、問題を解くときに、解法ではなく、考え方をノートに記すなど、汎用性のある考え方に意識を向けて学習するようにしていきましょう。

問題別寸評

[1]

(1)

四則演算の基本。　どうやったら楽に計算できるか、方針を立ててから手を付け始めるようにしましょう。

（2）

A：B＝3：9＝1：3　　A：C＝3：6＝1：2
より、C:D＝1：3（高さが等しいので）　　Dの面積は6㎠×3＝18㎠
A＋B＋C＋D＝3＋9＋6＋18＝36㎠
より、正方形の一辺は6㎝
Dのたては、Bのたてとの比により、9：18＝1：2
Dの横と、Bの横の比は、9：3＝3：1
よって、6㎝÷（1＋3）＝1．5㎝　
Dの横は、1.5×3＝3：4.5㎝
Dのたては、6㎝÷（1＋2）＝2㎝より、2×2＝4㎝
よって、Dの周りの長さは、（4.5＋4）×2＝17㎝

（3）

円ときたら、中心と円周上の点を結ぶ
これを思い出しましょう。複合図形は「わかる図形」に分解するということが基本です。円の中心と円周上の点を結ぶことによって、円、おうぎ形（半径と角度がわかるもの）、三角形、正方形、などなど、わかる図形に分解して面積をだすことを頭において解き進めてください。浦和明の星女子中を目指す受験生であれば、必ず解けるように練習しておきましょう。

（4）

比と個数を絡めた問題です。こちらも問題を読んですぐに解法が思いついて欲しい問題です。　完答目指して解ききりましょう。

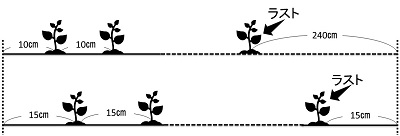
（5）

間の数と本数の数が逆比になる問題です。

10㎝ずつ間をあけて植えたとき、240㎝手前までしか植えることができなかったので、240㎝に植えるはずであった本数は、240÷10＝24　24－1＝23本（最後の端は植えないので、1を引きます）
また、15㎝ずつ植えていくと、1本余るので、10㎝ずつ植えるのと、15㎝ずつ植えるときの苗の差は、23＋1＝24本となります。
また、10㎝ずつと15㎝ずつ植えた時の間の比は、10：15＝2：3
本数の比は、端から端までのきょりはどちらでも同じなので、間と本数の比は逆比。
本数の比は、2：3なので、3－2＝1が24本に当たります。
24×2＝48本

（6）

条件にあてはまる数値、すなわち隣り合った2枚のカードの差になる数値をあてはめていきましょう。時間がかかってしまうようであれば、先の問題に進みましょう。
ただ、数値の感覚は、日ごろから養っておく必要があります。いくつか、試しながら正解をさぐっていくということも大切であるというメッセージが込められた問題でしょう。

（7）

正五角形の内角の和、折ったときに、どの部分がどこと重なるのかを考えて解きましょう。

［2］

（1）

アの部分の高さ10㎝のところまでに、30秒かかっているの、
（15×10×40）÷30＝200㎤/秒

（2）

水槽全体には、蛇口Aと蛇口Bの両方を使っているので、200×2＝400㎤/秒入っています。
（45×40×30）÷400＝135秒＝2分15秒

（3）

Aで30秒間入れると、
200×30＝6000㎤入りました。
45×40×24＝43200㎤・・・24㎝まで入れた時の体積
43200－6000＝37200㎤・・・これが、AとBで入れた体積になるので、
37200÷400＝93秒＝1分33秒
30秒+1分33秒＝2分3秒

［3］

（1）

三角数と四角数の総合問題です。　これは基本中の基本の問題なので、得点しておきたい問題です。

（2）

問題文にあることを、まずは手を動かして確認しましょう。
100番目の三角数は、（1+100）×100÷2＝5050
100番目の四角数は、100×100＝10000
10000－5050＝4950となります。
4950は実は、99番目の三角数となります。
また、200番目の三角数は、（1+200）×200÷2＝20100
201番目の四角数＝201×201＝40401
20100×2＝40200となり、40401－40200＝201

（3）

49番目の三角数＝（1＋49）×49÷2＝25×49＝1225
これを利用して、1225がどの平方数となるか求めると、25×49＝5×5×7×7＝35×35となるので、
5と7の平方数の積とわかります。よって、5×7＝35

［4］

［4］は合否を分けた一題として取り上げます。

［5］

［5］立体と規則性の問題です。
アは、直方体の表面積なので、解けてほしいところです。
イは、一番上のBをAに変えても、上から見た面の面積は変わりません。しかし、手前から見た面の面積は、Bの11枚と、Aの1枚に分けて考えます。Bの11枚は、アで求めた、側面積＝1×11×6×4＝264。一番上の段のAの側面積＝1×3×4＝12となり、求めた面積をすべて足します。

ウは、イで求めた面積に、上からも、下からも見えない、向かい合っている面＝（6×6－3×3）×2＝54を加えます。

エは、12÷2－1＝5個変えると表面積を最も大きくなります。
ウで求めたように、内側をBからAに変えると表面積は大きくなるので、12個中、一番上と、下の面をBとし、交互に挟むようにBをAに変えていくと、表面積は大きくなります。

オは、表面積は＝上下＋見えない部分＋Bの側面積＋Aの側面積
＝6×6×2＋（6×6－3×3）×10個＋1×6×4×7個＋1×3×4×5個＝570㎠

合否を分けた一題

（1）

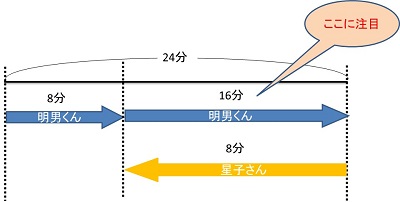
明男くんと星子さんは、8分で出会ったので、明男くんが24分でかかるきょりなので、
残りは、24－8＝16分で行きます。
16分で行くきょりを星子さんは8分で進んだので、
明男くんと星子さんの同じきょりにかかる時間の比は、8分：16分＝１：２
きょりが等しいので速さの比は逆比となります。
速さの比＝1：2

（2）

工事中だった区間での速さは、1/4になったということなので、（1）より星子さんの速さの②を利用して、

合計の時間と、合計のきょり、途中で速さを変えた、
というキーワードからつるかめ算であることに気づけたかが、ポイントです。

10×②－14＝6
6÷（3÷2）＝4分

応用問題も、やはり最後は「つるかめ算」という基本の考え方を使っています。
ただ、単純なつるかめ算ではなく、比を利用しなくてはいけないということが、やはり応用問題といわれるところです。処理の仕方、ここでは、きょりや速さを比で表して解くということも気づくべきポイントになります。
つるかめ算とわかっていても、どうやって表すのか、きょりが出ていない、速さも出ていないというときに、何を使うのか。このあたりは、日ごろから、比を利用して解く問題の練習をしておく必要があります。こういった問題の選定は、やはりプロしかできないことです。

浦和明の星女子中を目指す受験生の皆さんに、効率良く、良い問題を解いていくということを
受験ドクターでは行っています。ぜひ、お悩みなどございましたらご一報くださいませ！
講師一同、お待ちしております！！

著者：佐々木裕子

この記事は役にたちましたか？