算数の合否を分けた一題
聖光学院中入試対策・算数の合否を分けた一題(2020年度)
難易度分類
| [1] | (1) A (2) A (3) A |
|---|---|
| [2] | (1) A (2) A (3) A (4) B |
| [3] | (1) B (2) B (3) B (4) C |
| [4] | (1) (ア) A (イ) A (ウ) A (2) B |
| [5] | (1) A (2) B (3) B |
A…聖光学院中学合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、得点差がつかない問題
出題総評
学校側の発表によると、今年の4科合計の合格最低点は342点とのことです。
各教科の合格者平均は、国語が103.8点(150点満点)、算数が107.1点(150点満点)、理科が84.4点(100点満点)、社会が70.9点(100点満点)ということですので、合格最低点をこの各教科の合格者平均で比例配分すると、得手不得手を一切考慮せずに算数で取らなければならない最低ラインはちょうど100点程度――つまり、平均だけで単純に考えるなら、優しい問題から順に得点を積算していったときに100点を超える問題が「合否を分けた一題」となります。
ちなみに、合格者の最高点が150点と発表されていますので、少なくとも一人は満点だった受験生がいたということです。
例年より少しだけ難しめの問題だったことを考えると、お見事と言わざるを得ません。
さて、[1]が計算1題+小問集合2題、[2]~[5]が大問形式というおなじみの構成は、今年も例年通り踏襲されています。計算も、いつも通りの「逆算タイプ」のものに戻っています。
また、大問の出題内容も、[2]が調べ上げを含んだ「場合の数・数の性質」の問題、[3]が「速さ」の問題、[4]が「立体図形」の問題、[5]が「平面図形」の問題と、頻出単元通りの王道を行くものでした。
その意味では、聖光学院に向けて準備をしてきた受験生にとっては、予想通り、予定通りの問題だったでしょうから、純粋な実力勝負になったものと思います。
問題別寸評
(1)は基本通りの未知数を求める計算問題、(2)~(3)も、極めて基本的な一行問題でした。
ここは確実に得点しておきたいところです。
(1)
0.75や3.125などの小数は、すぐ分数に直せるように覚えておきましょう。計算の順序にさえ気をつければ、けっして難しくはありませんので、確実に正解してください。
(2)
規則のとらえ方が何通りか存在しますが、
1 | 2 , 1 , 2 | 3 , 2 , 1 , 2 , 3 | 4 , 3 , 2 , 1 , 2 , 3 , 4 | 5 , 4 , 3 , 2 , 1 , 2 , 3 , ……
というようなグループに分けるのが便利だと思います。
この形だと、グループごとの個数が 1個、3個、5個……というように奇数個になりますから、左端から各グループの最後までに並んだ数字の個数は、1個、4個、9個……と平方数になります。
2020に近い平方数を探すと、45×45=2025がありますので、45番目のグループの最後から6番目(あと5個残っているところ)が2020番目の数字となります。
45グループ目は、{45 , 44 , 43 , …… , 2 , 1 , 2 , …… , 43 , 44 , 45}という並びなので、最後の5個(41~45)を残す2020番目の数字は「40」です。
(3)
驚くほど基本的な時計算の問題です。
2時ちょうどの長針と短針の間の角は60度ですから、当然のことながら、長針が短針と重なる時刻の前後に両針の間の角が50度になる瞬間があり、答えは2つとなります。
確実に正解してください。
数の性質を上手に利用することで、ある程度の時間の短縮は図れますが、最終的には書きだすなどしなければならない問題も含んでいます。
いかに効率よく、ミスなく、確実に探せるかが勝負の鍵となります。
(1)
これは、問題条件をなぞらせる中で、出現する数の規則性に気づかせるというウォーミングアップ問題です。

この問題を通して、少なくとも「3の倍数しか出てこない」ということには気づいてください。
(2)
(1)に記載した通り、3を足しても3をかけても、元が3の倍数であれば3の倍数にしかなりません。この点に気づけば、3の倍数でない数が出てきたところで止めることができるので、333から逆算して戻っていく場合に無駄を省けます。
そうすると、3→9→12→36→108→111→333(B,A,B,B,A,B)の6回が最少とわかります。
(3)

(4)
操作は2種類しかありませんから、36から逆算して3までたどれる方法を探します。
このとき、途中の操作では「3の倍数」しか出現しないことを利用して、すべての場合を計算しなくてもすむように気をつけてください。
複雑な条件をいかに正確に整理できたかが明暗を分ける問題でした。このように、複雑に動くものの動きを正確につかむ必要がある問題では、ダイヤグラムが便利ですが、単に図に表すだけでなく、その上で上手に比を利用する必要があります。
本問の場合、条件が複雑なので、正確にダイヤグラムをかくことが大変です。また、解き方自体はそれほど難しくないのですが、ダイヤグラムの中に平行線がたくさんありますので、必要な相似や線を選び出すことが難しいでしょう。
実際に、問題文から分かることをダイヤグラムに整理すると下の図のようになります。
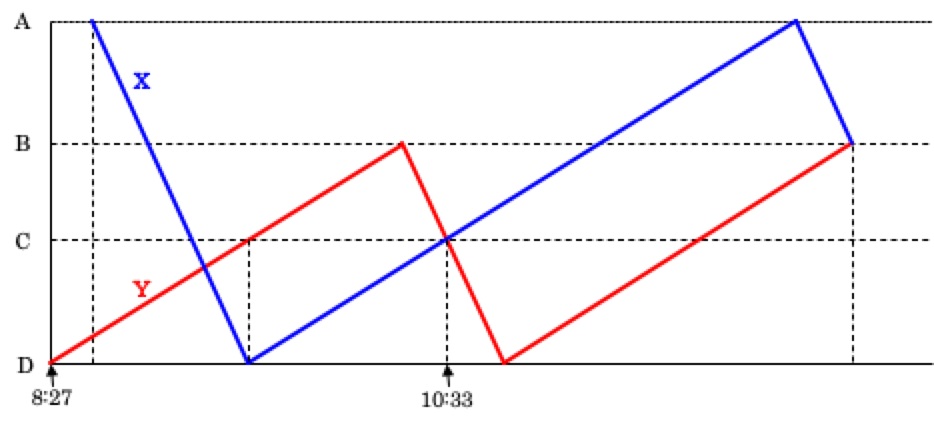
つまり、ダイヤグラムがきちんとできれば全問正解もねらえる一方で、ダイヤグラムが作れなければ全滅もありうる・・・・・・その意味では、非常に点差がつきやすい問題ですので、この大問3を「合否を分けた一題」とし、後ほどくわしく解説します。
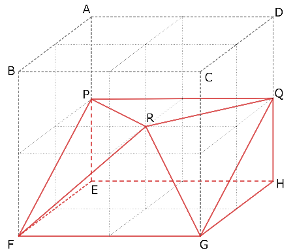
立方体の中空にある点Rを、しっかり想像できるかどうかが勝負のカギとなります。
また、実際に体積を出すときには、計算ができる形に上手に分割することが求められます。
(1)
投影図の問題としては割と基本的な形です。
聖光学院の受験生であれば、十分対応できる問題のレベルでしょう。
それだけにミスは許されません。
時間制限のある中でも、落ち着いて取り組みましょう。
立体Xを見取り図で表すと、右の図(赤線)のようになります。
(2)
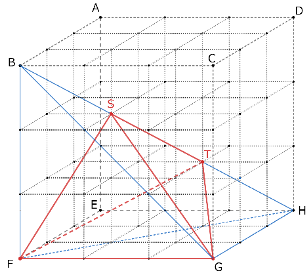
3等分点で作図をしなければならない分、(1)の問題よりは高度になりますが、投影図としては決して難しくありません。
立体Yを見取り図で表すと、右の図(赤線)のようになります。正しく想像できていたでしょうか。
この場合、三角形BFHを底面とし、点Gを頂点とする三角すい(青線部分を足したもの)を考えると、求める立体Yの底面FSTと高さが共通な三角すいであることが分かります。
BS:ST:TH=1:1:1より、底面積もちょうど3等分されていることに気づけば、比較的簡単に正解にたどり着くことができます。
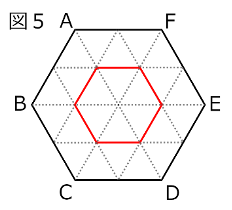
この問題のカギは、「正六角形の等分割」と、「等積変形」です。
解き方のコツに気付くことができれば、スムーズに正解にたどり着くことができるでしょう。
(1)
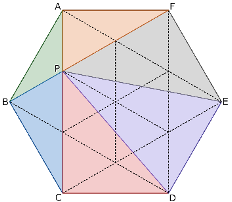
問題の指示通りに点Pをとると、上の図のようになります。
正六角形ABCDEFを、この図の点線のように18分割すると、ちょうどACとBFの交点が点Pになることが分かります。
ここで、三角形PABや三角形PBC、三角形PAFのように、18分割した三角形で表せるものは簡単ですが、それ以外の三角形は、等積変形を利用して面積の割合を求めてください。
(2)
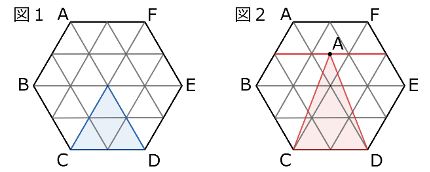
この問題では、条件に合うものをすべて答えなければなりませんので、どうすれ4分の1の面積を作れるかを考えなければなりません。
上の図1・図2は、ともに正六角形を24分割したものです。ここで、正六角形の4分の1の面積にするためには、24等分した図形6個分の大きさにすれば良いことになります。
図1の青い三角形は4個分ですから、必要な面積はこの1.5倍。そのためには、高さを1.5倍にすれば良いので、例えば辺CDを含む三角形が4分の1になるのであれば、点Pは図2の赤い直線上にあることになります。
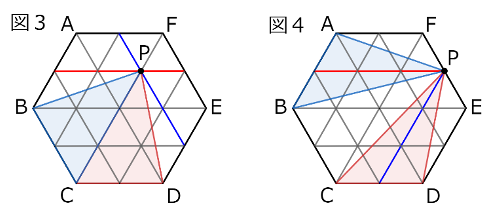
そして、そんな三角形が2つなければならないので、2つの方向からとった高さ1.5倍の直線(図2での赤い直線)の交点にPがあれば良いと分かります。
同じ分け方になるものをのぞくと、可能性があるのは図3・図4の2つのパターンとなります。
(3)
先ほどの(2)の問題で、面積4分の1を作るための条件が分かったと思います。カンで解かせるのではなく、あくまで条件考えさせるように、上手に誘導をしている良問といえるでしょう。
さて、4分の1を最大の面積にするためには、図4の三角形PBCのように、4分の1の三角形よりも高さが高いものを作ってはならないので、どの方向から見ても高さ1.5倍以内になるようにする必要があります。つまり、図5のように、正六角形のすべての辺を底辺としたときの「高さ1.5倍」となる直線(赤線)上のどこかに点Pがあれば、必ず4分の1の面積の三角形ができ、また、それよりも大きい面積の三角形は存在しないことになります。
合否を分けた一題
ある川の上流から順に,A,B,C,Dの4地点があり,船XはAD間を,船YはDB間を往復します。船X,Yは間の地点や折り返す地点ではとまらず,到着するとすぐに出発します。
ある日,午前8時27分に船YがD地点からB地点に向かって出発し,その何分か後に,船XがA地点からD地点に向けて出発しました。船Xと船Yがすれ違った後,船YはC地点を通過し,それと同時に船XはD地点に到着しました。船Xはすぐに折り返して出発したところ,B地点で折り返してきた船Yと,午前10時33分にC地点ですれ違いました。さらに,船XはA地点で折り返すと,D地点で折り返してきた船YとB地点で出会いました。
船Xと船Yの速さは等しく,上りは時速2km,下りは時速7kmで進むものとして,次の問いに答えなさい。
(1)BC間とCD間の距離の比を,最も簡単な整数比で答えなさい。
(2)船Xが初めてD地点に到着した時刻は午前何時何分ですか。
(3)船Yが初めてD地点に戻ってきた時刻は午前何時何分ですか。
(4)船Xが初めてA地点を出発した時刻は午前何時何分ですか。
【解法】
(1)
本文で示したダイヤグラムに、説明用の記号や色を加えたものがこちらです。
この図を利用して解説をしていきます。
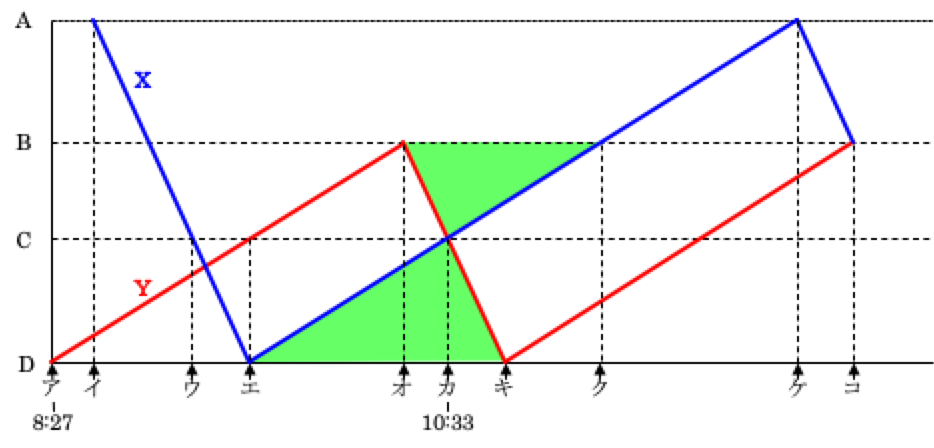
上のダイヤグラムで、エ~オは船YがC地点からB地点まで時速2kmで上るのにかかった時間、オ~カは船YがB地点からC地点まで時速7kmで下るのにかかった時間です。どちらもBC間の等しい距離を移動していますから、かかった時間の比は速さの逆比、つまり7:2となります。
同じように、エ~カは船XがD地点からC地点まで時速2kmで上るのにかかった時間、カ~キは船YがC地点からD地点まで時速7kmで下るのにかかった時間ですから、やはり7:2です。
この比を合成すると、エ~オ:オ~カ:カ~キ=49:14:18となりますので、オ~カ:カ~キ=7:9。これは、黄緑の三角形の相似比となりますから、BC:CDも7:9です。
(2)(3)
まったく同じ要領で、ア~オは船YがD地点からB地点まで時速2kmで上るのにかかった時間、オ~キは船YがB地点からD地点まで時速7kmで下るのにかかった時間ですから、やはり7:2です。
これを、(1)で作ったエ~オ:オ~カ:カ~キ=49:14:18と合わせると、ア~オ:オ~カ:カ~キ=112:14:18となります。
ここで、アが8時27分、カが10時33分であることから、ア~カは126分なので、ア~オ=112分、オ~カ=14分、カ~キ=18分、エ~オ=49分と求められます。
したがって、エ~カ=63分ですから、船XがはじめてD地点に到着した時刻エは午前9時30分です。
また、カ~キ=18分ですから、船Yが初めてD地点に戻ってきた時刻キも、午前10時51分と求められます。
(4)
先ほどの問題で分かった時刻を図に書き入れていくと、次のようになります。
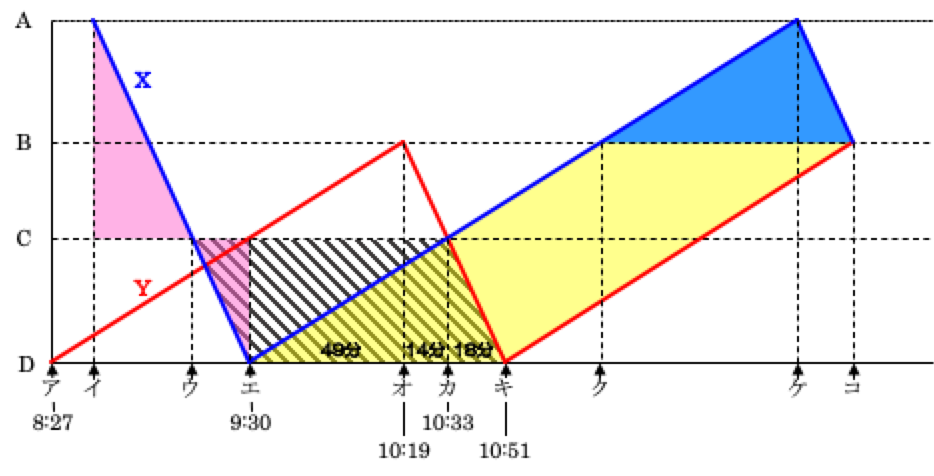
どちらの船も速さは等しいので、右上がりの線どうし、右下がりの線どうしは、それぞれ平行になっています。つまり、図の斜線部分は平行四辺形なので、ウ~エ=カ~キ=18分と分かります。
また、黄色の部分も平行四辺形ですから、斜線部分の平行四辺形と黄色の平行四辺形が重なった三角形と、青色の三角形とが合同となり、AB間の距離がCD間の距離と等しいことが分かります。したがって、(1)の結果と合わせると、AB:BC:CD=9:7:9です。
ここで、ピンク色の三角形の部分は相似ですから、その相似比は(9+7):9=16:9なので、イ~ウ:ウ~エ=16:9。ウ~エ=18分であることから、イ~ウ=32分、つまり、イ~エ=50分ですから、船Xが初めてA地点を出発した時刻イは午前8時40分です。
(答え) (1)7:9 (2)午前9時30分 (3)午前10時51分 (4)午前8時40分
聖光学院中入試対策・関連記事一覧
聖光学院中入試対策・同じ教科(算数)の記事
聖光学院中入試対策・同じテーマ(合否を分けた一題)の記事
- 社会の合否を分けた一題(2010年度)
- 算数の合否を分けた一題(2015年度)
- 国語の合否を分けた一題(2015年度)
- 社会の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2021年度)
- 算数の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)