算数の合否を分けた一題
東海入試対策・算数の合否を分けた一題(2018年度)
難易度分類
| 1 | (1)A (2)B |
|---|---|
| 2 | B |
| 3 | (1)A (2)A |
| 4 | (1)B (2)C |
| 5 | (1)A (2)C |
| 6 | (1)B (2)C |
| 7 | (1)A (2)B (3)B |
A・・・東海中学を目指すなら確実に正解したい問題
B・・・解法によって、得点、解答時間に差がつく問題
C・・・難易度、処理量などから失点もやむない問題
出題総評
例年と同じ出題形式で、テスト2の1は易しく、テスト2の2は難問が多いテスト構成でした。解答用紙の裏面が計算用紙となるため、裏面も採点される可能性があることを意識した使い方を徹底したいです。今年度は、図形の問題と条件整理の問題に解き難い問題が多く出題されました。日ごろから、図形の問題や、表などを利用して条件整理の問題を解く練習を行う必要があるでしょう。また、いろいろ試すことによって解ける問題も出題されているため、泥臭く問題を解いていく根気強さも入試までに身に着けたいところです。
問題別寸評
(1)例年と同様の「小数と分数の四則演算」です。日頃から小数から分数、場合によっては分数から小数への変換をスムーズに行うことが出来るよう、計算練習を行いましょう。確実に正解したい1問です。
(2)「条件整理」の問題です。与えられた条件から、50円切手をもっとも多く使用した場合の切手の組み合わせ方が7枚であることがわかります。切手の枚数を少なくするためには、なるべく高い切手を多く使用する必要があるため、92円切手、82円切手、62円切手から順に使用する切手の組み合わせを考えていくことで、問題を解いていきましょう。多少時間がかかるため、一回の作業で正解したい問題です。
「条件整理」の問題です。約数の個数に関する基礎知識を利用して、条件を整理し、最後は自力算を利用して問題を解く必要があるため、試行力が試される問題です。試行の量はそれほど多くないので、与えられた問題の条件を正確に整理できれば、問題を解くことができるでしょう。問題を解くために必要な条件は、小学生であること、長男・次男・三男の年齢の関係、約数の個数です。
(1)「比の利用」の問題です。与えられた問題文から線分図を用いて、初めに水そうに入っている水の量の比と、これから加わる水の量の比、水そうの容積の大きさの比を合わせることができれば、(2)の問題まで解くことができるでしょう。比を合わせることに慣れていれば、比較的得点し易い問題だと考えられます。
(2)(1)で比を合わせたあとの水そうの容積比と、問題文で与えられた本物数字(実数)を対応させることで、水そうがいっぱいになるまでにかかる時間を求めることができます。(1)を解くことができていれば、比較的解き易い問題だと考えられます。
東海中学では定番の「平面図形」の問題です。平面上の線の数が多いため、問題を解くために必要な情報だけ見る技術が必要になります。
(1)「相似」を利用した問題となります。辺DEを延長し、辺BCとの交点をHとします。そして、三角形ADEと三角形BHEの相似比から辺BHの長さを求めます。そうすると、三角形FDGと三角形CHGの相似比から三角形BCGの高さを求めることができ、三角形BCGの面積を求めることができます。
(2)「角度」の問題です。ヒントとなる角度が少ないことから、「特殊な三角形」の辺の比から角度を求める必要があることに気づきましょう。解き難い問題です。正答率は低いものと考えられます。
東海中学では定番の「立体図形」の問題です。体積と表面積の問題ですが、テキストなどではあまり扱うことの無い問題でした。受験生にとっては初見の問題となったでしょう。
(1)問題文で与えられた表面積の差180㎠が、底面の何枚分にあたるかを考えることで問題を解くことができるでしょう。真上から見た図から、二等辺三角形の各部分の面積比を求め、1段目から4段目までの表面積にあたる部分(共通部分は除く)がいくつ分あるのかをカウントするようにしましょう。
(2)三角柱の側面の比を①とし、(1)で求めた三角柱の底面積の大きさとの和を求め、問題文で与えられた全体の表面比を対応させ問題を解きましょう。
「平面図形」と「立体図形」の問題です。平行四辺形が直方体の側面になることがイメージしづらい受験生が多かったと推察されます。問題文をすんなりと理解することができれば、解法を考えることができるでしょう。わからない場合は、実際に折り紙などを使って、平行四辺形が直方体の側面になることを目で確認しましょう。
(1)底面が正方形で体積の大きさがわかっているので、頂点Aから辺CDに引いた垂線(直方体の高さ)を逆算を用いて12㎝と求め、平行四辺形を長方形と変形させることで、平行四辺形ABCDの面積が108㎠であることがわかります。その後、逆算を用いて辺ADの長さを求めることで、辺EDの長さを求めることができます。
(2)(1)からAPの長さは頂点Aから辺CD上に引いた垂線と辺EFとの交点と頂点Aまでの長さであることがわかるため、相似な図形の相似比を利用することでAPの長さを求めることができます。
(1)~(3)「条件整理の問題」です。合否を分けた一題で扱います。
合否を分けた一題
与えられた問題文の意味を理解するのに時間がかかるでしょう。問題文が理解できたとしても、効果的な表を作成することが出来なければ、かなりの時間を消費してしまう問題です。A、P、Q、Rから乗った乗客が何区間バスに乗ったかがわかる表を作成し、降車人数を確認しながら、与えられた条件に合わせて問題を解く必要があります。3つ以上の条件に照らし合わせながら問題を解いていきますので、表の作成は必須です。
問題文から以下のような表(乗車地点と乗車人数、乗車区間)を作成することができます。
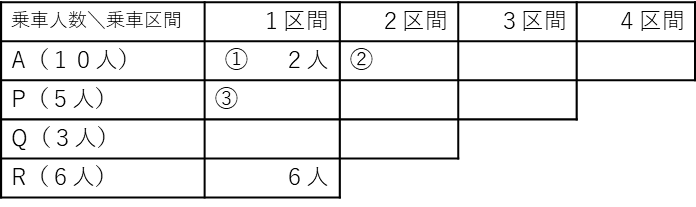
(1)A~Qまで2区間だけ乗った人数が、A~Pまでの1区間だけ乗った人数とP~Qまでの1区間だけ乗った人数の合計と同じでした。
という問題文で与えられた条件より、①と③の部分の人数の和が、②の部分の人数と等しいので、その点について考えてみましょう。ここで重要なポイントは問題文で与えられた、Q地点で降車した人数が4人だということです。
つまり、②と③の合計は4人だということに気が付くことができると正解までたどり着くことができます。
以下の表は、①と③の和が②と等しく、②と③の和が4人となる場合のものです。
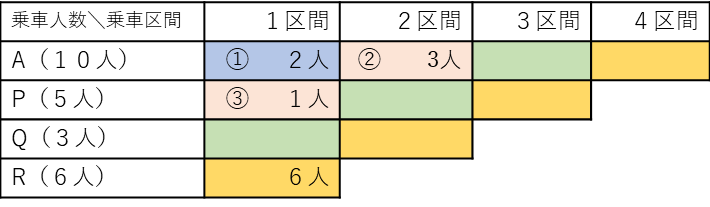
この表から、(1)の答えはAから乗った人・・・3人 Pから乗った人・・・1人となります。ここで表内の色分けされた枠が、問題文の条件から、以下の事を表すこと、
青・・・Pで降車した人数(合計 2人)
赤・・・Qで降車した人数(合計 4人)
緑・・・Rで降車した人数(合計 7人)
橙・・・Bで降車した人数(合計11人)
この点に気づくことが出来れば、(2)(3)ともスムーズに問題を解くことが出来るでしょ
う。この気づきが(2)(3)の出来を分けると考えられます。
(2)3区間だけ乗った人数の合計と4区間だけ乗った人数は同じで、2区間だけ乗った人数の合計は、3区間だけ乗った人数の合計の2倍より1人多かった。
という問題文ですが、少々複雑で、思考が止まってしまいます。段階に分け考えていきましょう。
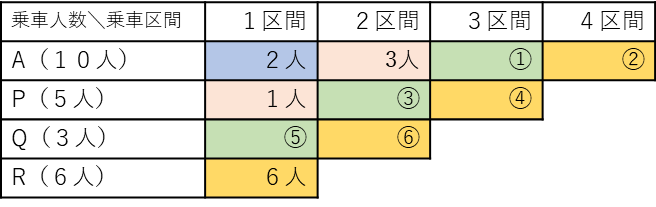
まず、①と②の合計が5人になり、③と④の合計が4人、①と④の合計が②と等しくなる場合を考えましょう。
[①が1人の場合]
② 4人
③ 1人
④ 3人
となります。
さらに、(2)の問題文の条件、色分けされた部分の合計人数、⑤と⑥の和が3人となる、これらをともに満たす人数の分け方を考えてみると・・・条件を満たすものは、無いようです。他の場合を考えてみましょう。
[①が2人の場合]
② 3人
③ 3人
④ 1人
となります。先ほどと同じように、(2)の問題文の条件、色分けされた部分の合計人数、⑤と⑥の和が3人となる、これらをともに満たす人数の分け方を考えてみると・・・以下のようになります。
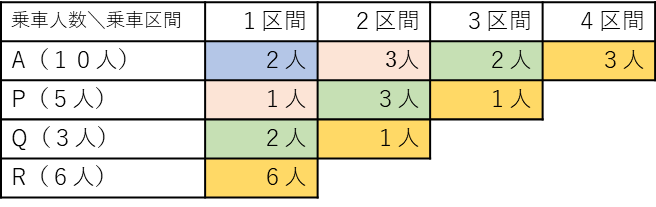
一度出来上がったと思った表でも、必ず見直しが必要です。
横に表を見ていくことで、各地点からの乗車人数と降車人数に間違いがないかを確認します。
A 10人(降車総数)
P 5人(降車総数)
Q 3人(降車総数)
R 6人(降車総数)
表の各地点からの乗車人数と比較すると、間違いはないようです。
次に、色分けされた部分の合計人数を問題文の内容に沿って確認します。
唯一、B町での降車人数のみ、「全員降りました」という表現になっていますが、乗車総数とR地点までの降車総数からB町での降車人数が11名だとわかります。
p 2人降車(青 2人)
Q 4人降車(赤 4人)
R 7人降車(緑 7人)
B 11人降車(橙 11人)
問題文の表記からわかる各地点の降車人数と、作成した表からわかる各地点の降車人数が一致するため、こちらも間違いはないようです。
最後に、(2)の問題文条件((1)の問題文の後)との整合性を確認しましょう。
(2)の問題文の条件である、3区間だけ乗った人数と4区間だけ乗った人数の合計が同じであることは、表より共に3人であるため条件を満たしています。
さらに、2区間だけ乗った人数の合計は、3区間だけ乗った人数の合計の2倍よりも1人多かったという条件も、2区間だけ乗った人数(7人)と3区間だけ乗った人数(3人)であるため、条件を満たします。
これらのことから、表の作成に誤りが無いことがわかるため、表の左端部分の合計人数から
(2)の答えは、11人となります。
(3)Bで降りた人のうち、Aから乗った人とPから乗った人とQから乗った人はそれぞれ何人ですか。
この問いに関しては、(2)の問題での表の作成が役に立ちます。(2)を解いた生徒にとってはすでに答えがわかっている問題となります。ご褒美問題ですね。(3)の答えは、Aから・・・3人 Pから・・・1人 Qから・・・1人となります。
合否を分けた一題で扱った問題は最終問題となり、一見かなり難しそうな印象を受け敬遠しがちです。しかし、効果的な表を作成することが出来れば、さほど多くない試行量で問題を解くことができるため、間違いなく合否を分ける一題でした。中学受験において、表の作成や作図がいかに重要か考えさせられる一題です。


 (3 投票, 平均値/最大値: 3.67 / 5)
(3 投票, 平均値/最大値: 3.67 / 5)