算数の合否を分けた一題（2020年度）

算数の合否を分けた一題

フェリス女子中入試対策・算数の合否を分けた一題（2020年度）

難易度分類

［1］	(1)A　(2)A　(3)B　(4)A　(5)ア…B　イ…C
［2］	(1)A　(2)B
［3］	(1)A　(2)A
［4］	(1)A　(2)A　(3)C
［5］	(1)B　(2)C (3)C

Ａ：フェリス合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断してとばすべき問題

出題総評

昨年に引き続き、今年も大問1は計算を含む小問が全5問、大問2～5は4つの単元にわかれて、という昨今の形式が踏襲された入試となりました。
詳細については大問1が逆算・平面図形・数の性質・割合・場合の数、大問2は規則性、大問3は平面図形の基本問題、大問4は数の操作、大問5は和差の応用問題でした。

問題別寸評

［１］

(1)は分数と小数の逆算、(2)は平面図形（角度）の問題、(3)は素因数分解を用いた数の性質の問題、(4)は割合（倍数算）の問題、(5)は場合の数の問題でした。
(1)分数と小数が入り混じっているので、必ず分数に統一して逆算をするようにしましょう。時間の目安は2分ほどです。

(2)角BDCが180-(104+38)=38°なので、ここから三角形BCDは二等辺三角形であることがわかります。また、三角形ABCが正三角形なので、AC=BC=CDで三角形ACDも二等辺三角形であることがわかります。ここからあの角の大きさが計算を進めるとわかります。典型題ですから、確実にとるようにしましょう。

(3)回答までの手順が少々複雑な問題です。《2》×《3》×《4》×…×《10》は、2が9個、3が8個、4が7個、5が6個、6が5個、7が4個、8が3個、9が2個、10が1個かけあわさったものです。この中で素数でない数に着目します。4=2×2なので、4が7個ということは2が14個あると解釈します。同じようにして、6・8・9・10も整理していくと2が38個、3が17個、5が7個、7が4個あるとわかります。BをかけたらCの立方数となったことから、例えば2は38÷3=12…2となり、余りが2であるのでC×C×Cとするためには2が1個不足していることとなります。同様に3・5・7についても調べ、各々の数をかけあわせたら答えが求まります。考え方がすぐに思い浮かばないようであれば、後回しにすべき一問です。

(4)A、Bの情況について式を立てると
A ⑨+16= 17
B ⑦+12= 13

ここから倍数変化算として処理をすれば答えが求まります。こちらも典型題なので落とせません。

(5)矢印の向きから、その置き方を考える場合の数の問題ですが、イは場合分けを多岐に渡ってしなければならず、面倒なのでアだけを得点できればよいかと思われます。
ア　←を〇、→を×とします。矢印が向き合ってはいけないので、×が〇よりも左側にきてはいけないことになります。並び順は〇〇〇〇〇〇〇、〇〇〇〇〇〇×、〇〇〇〇〇××、…、×××××××となり答えが求まります。
イ　アより、並び方は〇6個・×1個、〇5個・×2個、〇4個・×3個、〇3個・×4個、〇2個・×5個、〇1個・×6個のいずれかです（矢印のうち、1組だけが向き合うので〇だけも×だけもありえません）。次に、それぞれの場合に分けて題意に沿う並べ方を考えると、順に6通り、5通り、12通り、12通り、15通り、6通りとなって答えが求まります。場合の数という単元もさることながら、答えに至るまでの道筋がかなり煩雑なものとなるので、とばした方が無難です。

［2］

ここからは大問になります。2点の移動が絡んだ規則性の問題です。今年は本問を、合否を分けた一題として詳細を後述します。

［3］

おうぎ形が絡む平面図形の問題ですが、本校の入試の大問3は確実にできなくてはならない典型題である傾向にあります。
(1)半円の中心をOとし、そこから真上に向かって直線を引くと以下の図のようになります。

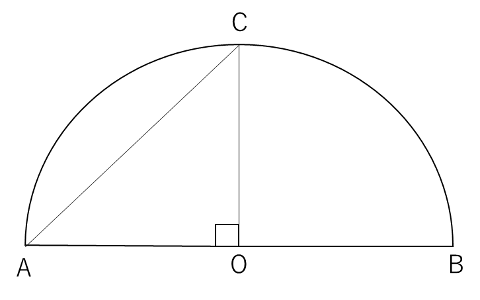
半径3㎝、中心角90°のおうぎ形AOCから、直角二等辺三角形AOCを引いて答えを求めます。

(2) 半円の中心をOとし、そこから右上に向かって直線を引くと以下の図のようになります。

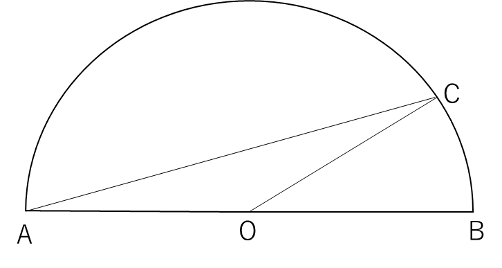
三角形AOCに着目すると、AO=CO=3㎝なので二等辺三角形です。角OAC=角OCA=15°なので、角AOC=180-15×2=150°となります。半径3㎝、中心角150°のおうぎ形AOCから、底辺が3㎝の三角形AOCを引いて答えを求めます。三角形AOCの高さについては、角COBが180-150=30°であることから、30°の利用を用いると3÷2=1.5㎝と求まります。

［4］

数の操作に関しての問題です。複雑な計算を要するので、誘導が与えられている(2)まで解ければ十分でしょう。

［5］

和と差について考える文章題ですが、推理もしなくてはならないために最終問として難易度が高くなっています。
(1)Xさんの所持金がわからないので、具体的に例をおいて考えていくとよいでしょう。
①a＜b＜cのとき
X=1000円とすると、a=1600-1000=600円、b=3000-1000=2000円、c=4000-1000=3000円となるので成立します。
③b＜a＜cのとき
X=2400円とすると、a=2400-1600=800円、b=3000-2400=600円、c=4000-2400=1600円となるので成立します。
④b＜c＜aのとき
X=2900円とすると、a=2900-1600=1300円、b=3000-2900=100円、c=4000-2900=1100円となるので成立します。
⑥c＜b＜aのとき
X=3800円とすると、a=3800-1600=2200円、b=3800-3000=800円、c=4000-3800=200円となるので成立します。
②a＜c＜bのときと⑤c＜a＜bのときはXがどのような値であっても成立しません。

(2)xを①円とします。(1)より②、⑤を省いた①、③、④、⑥の中で考えていきます。
・①a＜b＜cのとき
a=1600-①
b=3000-①
c=4000-①
とおけるので、bとcの和は7000-②、aの2倍は3200-②となりますが、この2つが同じになることはありえません。

・⑥ｃ＜b＜aのとき
a=①-1600
b=①-3000
c=4000-①
とおけるので、bとcの和は1000、aの2倍は②-3200となり、②-3200=1000で①=2100となりますが、この場合はbが計算できないのでありえません。

・④b＜c＜aのとき
a=①-1600
b=3000-①
c=4000-①
とおけるので、bとcの和は7000-②、aの2倍は②-3200となり、②-3200=7000-②で①=2550と計算できますが、この場合はa=950、b=450、c=1450となり、b＜a＜cとなるので矛盾します。

・③b＜a＜cのとき
a=①-1600
b=3000-①
c=4000-①
とおけるので、bとcの和は7000-②、aの2倍は②-3200となり、②-3200=7000-②で①=2550と計算できます。この場合はa=950、b=450、c=1450となりb＜a＜cが成立します。

(3)先ほどの問題から、③の時であるとわかり、Xさんの所持金も求まります。

合否を分けた一題

前半の大問群の中で、今回は大問2を合否をわけた一題として紹介しましょう。2点の動きを考える点の移動を題材にしたもので、動きの規則を正確に読み取る必要がある重要な問題と言えます。

［2］点の移動・規則性

(1)まず、AB=FB=12㎝なのでPもQも12÷12=1秒後にBで出会うことになります。その状態からPは1秒ごとにC→D→E→F→A→B(6秒で元の位置に戻る)と移動し、Qは1秒ごとにD→F→B→D→F→B(3秒で元の位置に戻る)と移動するので6と3の最小公倍数で6秒ごとに同じ点で出会うことになります。出発してからの時間とP・Qがいる頂点をまとめると以下の表のようになります。

以上から答えが求まります。
答え：ア…B　イ…1　ウ…6
(2) PとQが出会う可能性があるのはBかDかFです。その3点のいずれかに、PとQが着く時間を調べます。Pについては1つの頂点間を移動するのに12÷3=4秒かかるので、Pは4秒後にB、その8秒後である12秒後にD、20秒後にF…と動いていくことになります。Qについては1つの頂点間を移動するのに12÷4=3秒かかるので、Qは3秒後にB、その3秒後である6秒後にD、9秒後にF、12秒後にB…と動いていくことになります。まずは同じ時間である12秒後を起点とし、8と3の最小公倍数である24秒ごとにPとQがどの位置に来るかを調べていきます。出発してからの時間とP・Qがいる頂点をまとめると以下の表のようになります。

ここから、2点が初めて出会う場所は頂点Dで、60秒後のことであるとわかります。また、PはDから変わらないので、Qが次にDにくるときを考えると、B→F→D→B→F→D…という動きになっているので24×3=72秒ごとであることもわかります。
答え：エ…D　オ…60　カ…72