算数の合否を分けた一題（2018年度）

算数の合否を分けた一題

世田谷学園中学入試対策・算数の合否を分けた一題（2018年度）

難易度分類

［１］	（１）A　（２）A　（３）A（４）A（５）A
［２］	（１）A（２）B
［３］	（１）A（２）B
［４］	（１）A　（２）B
［５］	（１）A　（２）B
［６］	（１）B（２）B

Ａ：世田谷学園中を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、一旦とばすべき問題

出題総評

例年と同じ問題数、難易度の構成でした。
学校説明会で先生がおっしゃるように、入試で定番とされる問題（典型題と言われる問題）をきちんと学習していけば十分に合格点に達します。［１］は日課の計算テキストの1行題で見かけたことのある問題でしょう。ですが、微妙に計算力が求められるような数字に設定されていたりするので、なめてかかることは禁物です。世田谷学園合格者は、ここはしっかり満点ベースで取り切る生徒がほとんどでしょう。例年［２］～［６］にかけては、すこし難しい問題が出題される事があり、合格者と不合格者で差が付きやすい傾向にあります。
今年は［５］のニュートン算が特に大きく合否に影響したと思われます。ニュートン算は、いわゆる典型題の一つですが、最初の理解の壁が厚いため多くの受験生が苦手なまま放置した状態で入試に臨みがちです。このような問題にじっくりと腰を据えて取り組んできたかどうかで入試の結果が分かれると言ってよいでしょう。

問題別寸評

［１］

（１）

8/25÷0.125のところで、8/25÷1/8＝1/25としてしまわないように注意です。
　→答え4

（２）

消去算で解くとよいですが、数字は若干面倒な設定になっています。注意深く計算する力が求められます。
→答え420円

（３）

順に2/3をかけていって求めましょう。
→答え38㎝

（４）

増えたマッチ棒に着目していきましょう。２番目は１番目＋６本、３番目は２番目＋８本、４番目は３番目＋10本となっていますので、10番目の図形は9番目＋22本となります。
4＋6＋8＋10＋12・・・＋22＝（4＋22）×10÷2＝130本
→答え130本

（５）

15勝ずつしたときに差はありません。Aの勝ちを1つ多くすると、Bの負けが1つ増えるので、2人の差は（2＋1）×2＝6点広がります。
　12点差なので、12÷6＝2より、Aの勝ちは15＋2＝17回です。
→答え17回

（６）

OA＝DEより、DEも半径と同じ長さであり、△EDOが二等辺三角形であることに気付きたいところです。
→答え18°

［２］

旗を立てる問題は、倍数の問題に置き換えて考えます。
赤の旗は５mおきにたてます。120÷5＝24　なので、赤の旗は25本立ち、その場所は0、5、10、15、20、25、…、120　です。

（１）

黄色の旗も同様に考えると、120÷3＝40　40＋1＝41本です。　したがって黄色の旗を立てる場所は、0、3、6，9、12、15、…120 ですが、すでに赤があるところにたててはだめです。そのような場所は、3の倍数と5の倍数が重なるところなので、15の倍数ごとにあります。
120÷15＝8　8＋1＝9本（はしっこの0と120も含む）
41―9＝32本
→答え32本

（２）

１ｍおきに旗をたてた場合の本数は、120÷1＋1＝121本ですが、すでに赤と黄色があるところには立てません。
赤と黄色の本数の合計は、25＋41―9＝57本なので、
121―57＝64箇所に青を立てることになります。
→答え64本

［3］

（１）

容器前面の五角形を底面積として考えましょう。
224÷（8×5＋2×8）＝4
→答え4㎝

（２）

水が残っている部分が２箇所に分かれています。この二つは１：２の相似な三角形です。（面積比は１：４）また、床と容器の間にできた隙間部分の空洞は水が残っている部分の大きな方と合同であることに気付きましょう。
空洞部分の体積は、３×８÷２×４＝４８㎤
したがって、水の小さい方は、４８÷４＝１２㎤となり、
残った水の合計は、１２＋４８＝６０㎤です。

［４］

（１）

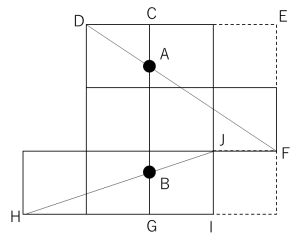
△CADと△EFDの相似を利用して、CAを求めると、CA＝１２×１／３＝４㎝
同様に、△JHIと△BHGの相似を利用して、BGを求めると、６×２／３＝４㎝
AB＝１８―（４＋４）＝１０㎝

（２）

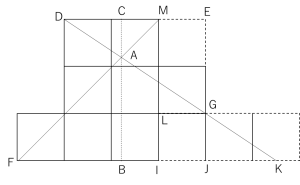
考え方自体は難しくありませんが、途中の計算で数値が複雑になりがちなので、そこを上図に処理する力が求められます。
図のように延長し、先にJKを求めます。
△DGEと△KGJは相似比２：１なので、
JK＝１８÷２＝９㎝、FK＝２４＋９＝３３㎝
次に、△DAMと△KAFの相似を利用して、
ABを求めます。
DM：FK＝１２：３３＝４：１１より、
AB＝１８×１１／１５＝66／5

斜線部分は、△AFKから正方形１つと△GJKを引いて求めます。
３３×66／5÷２―（６×６＋９×６÷２）
＝２１７．８―（３６＋２７）＝１５４．８㎠

→答え：１５４．８㎠

［５］合否を分けた一題として次のページで扱います。

［６］

時計算と同じように、１秒間に回る角度（角速度）を使って考えると、スッキリと考えることが出来ますが、ある程度慣れておく必要があるでしょう。この問題ではあまり差が付かなかったかもしれません。

（１）

Pの角速度は３６０÷６０＝６°/秒、Qの角速度は３６０÷４０＝９°/秒　です。
△OPQが直角三角形になるのは、∠POQが90°になるか、∠PQOが90°になるかのどちらかですが、先に起こるのは∠PQOが90°になるときです。このとき、PとQは合わせて60°移動します。
６０÷（６＋９）＝４秒後
→答え４秒後

（２）

PかQの位置を動かさずに考えましょう。仮にPを動かさないようにすると、Qは９＋６＝１５°ずつ、Aから反時計回りに動いているのと同じことになります。
１０秒後は、Aから１５０°左に回った位置にあります。
このとき、QからAOに垂直に下ろした垂線をQHとすると、３０°、６０°、９０°の直角三角形ができますので、QHは８÷２＝４㎝とわかります。
従って、△OPQの面積は１６×４÷２＝３２㎠です。

合否を分けた一題

典型的なニュートン算でしたが、最初に並んでいる行列の人数が示されていないので、比を使ってこの量を決めておく必要があります。
ニュートン算で差が付くのはこの部分ですので、世田谷学園に限らずしっかりと根本原理を理解しておきたいものです。

［５］

１分間に行列に並ぶ人の人数を①とします。
窓口が１つのときの、１分間の処理量は、１０―①　→３０分かかる
窓口が２つのときは、２０―①　→１０分かかる