算数の合否を分けた一題（2019年度）

算数の合否を分けた一題

世田谷学園中学入試対策・算数の合否を分けた一題（2019年度）

難易度分類

１	（１）A　（２）A　（３）A 　（４）A　（５）A　（６）A
２	（１）A　（２）A
３	（１）B　（２）B
４	（１）A　（２）A
５	（１）B　（２）C
６	（１）A　（２）C

A…世田谷学園中合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題

問題別寸評

１

（１）

四則演算の問題

（２）

40÷5＝8　と　40÷4＝10　より、下りと上りの時速を求めることが出来る。
下り：「静水時の速さ」+「流速」＝8
上り：「静水時の速さ」×2-「流速」＝10
より、2本の式を足すと、流速が打ち消されるので、「静水時の速さ」×3＝18となります。
よって、静水時の速さが18÷3＝6　より、時速6㎞です。

（３）

もし、売れ残りの20個も売れていたら利益はいくらだったか？と考えます。「仕入れの総額」－「売り上げの総額」＝「利益」　であり、これが現在14400円です。残りの20個が売れた場合、仕入れ金額は変わりませんが、売り上げが20個分増えます。つまり、　360×20＝7200円　14400+7200＝21600円の利益が出ることになります。
これは全部売った場合の利益ですので、「売れたときの一個当たりの利益」で割ると個数が求められます。よって　21600÷（360-180）＝120　より、全部で120個仕入れています。

（４）

問題で聞かれていることは何分後かですが、まずは8％の食塩水を何ｇ入れればよいかを求めましょう。その後で、答えの形式に合わせて、時間を求めます。
問題を単純化すると「3％の食塩水200gに8％の食塩水を何g混ぜると、6%になりますか」
です。これは面積図やてんびん図を使って求めると、300gだと分かります。よって、300÷10＝30分後　となります。

（５）

全体の仕事量を設定し、それに合わせて兄弟の一日の仕事量を用いて計算していく問題です。全体の仕事量は「1」としても良いですし、分数を避けるために「30」としても良いです。（もちろん1や30以外にもどのような数に設定しても解けますが、計算が複雑になるためお勧めしません）
今回は全体の仕事量を30としましょう。兄の一日の仕事量は3、弟の一日の仕事量は2となります。
さて、問題より、最後に弟が一人で12日働いているので、この間の仕事量は2×12＝24です。
30-24＝6　より、兄が□日で働いた仕事量は6です。　よって　6÷3＝2　より、兄が働いた日数は2日です。

（６）

平面図形のひとつの角度が60°と分かっているので、もう一つの角が120°だという所がポイントです。後はABとACの長さが等しいことを利用して二等辺三角形として、48°と求めます。

２

（１）

2つ余っているのでボールは　210-2＝208　個使っています。　208÷4＝52　52+1＝53　より、一辺は53個です。

（２）

正方形を作るのに必要なボールの個数を表にまとめ、規則性を探ります。すると

番目	1番目	2番目	3番目	4番目	・・・
個数	4個	8個	12個	16個	・・・

よって、220個のボールで出来るだけたくさんの正方形を作るということは

4+8+12+16+・・・+□　が、220以下で最も近くなる時を探せば、答えを求めることが出来ます。ひとつの解法としては、地道に足していき、220に近づく時を探す方法です。
入試の本番では、こちらの方法で構わないでしょう。ですが、せっかくなので計算で求める方法で解説致します。

番目	1番目	2番目	3番目	4番目	・・・
個数	4個	8個	12個	16個	・・・
規則	4×1	4×2	4×3	4×4	・・・

上の表のようになります。よって
4+8+12+16+・・・
＝（4×1）+（4×2）+（4×3）+（4×4）+・・・
＝4×（1+2+3+4+・・・）
上の式の答えが、220に近づく時を探せばよいと分かります。
220÷4＝55　と割り切れます。よって、
4×（1+2+3+4+・・・）＝220　より
（1+2+3+4+・・・）の部分が55となります。
1から10まで足すと55になる、ということは覚えているかと思います。
よって、作れる正方形は1～10までの10種類です。

３

（１）

流水算の問題ですが、この問題は「～回こぐ」という表現が使われています。流水算の典型題では、「流速が変わる」や「エンジンの出力（速さ）が変わる」といった形式の問題は見慣れているはずです。今回の「～回こぐ」とは、何を表しているのか？ここから考えていきます。
この問題文は「静水時にA地点からB地点までと同じ距離を移動するには、何回こげばよいですか。」とあります。ここで戸惑った受験生もいたかもしれません。つまり、距離はA地点からB地点までの距離で特定されている。しかし、それにかかる時間が指定されていないのに、速さを求められるはずがない。というものです。つまり、「～回こぐ」という表現が、典型題と同じように、速さの変化を表す文だと捉えてしまうと、意味を理解できなくなってしまいます。
本問の「～回こぐ」は、一回こぐごとに一定の距離を進んでいく、という条件設定を表しています。つまり、カヌーを漕いだ回数で速度が変わるのではなく、一回漕ぐごとに〇m進む、といったイメージです。
この理解を元に、計算を進めていきます。
まず、A地点からB地点までの距離を設定します。問題文に「30秒」と「50秒」とあります。距離を30と50で割ることになりそうなので、今回はAからBまでの距離を「150」と設定します。
※実際には30で割る計算は行わないので、全体の距離は50とした方がきれいに計算できますが、試験中にそこまで見通せることは少ないと思われますので、今回は150に設定して解説します。
カヌーを漕がない場合は、150÷50＝3　の速さで下っていきます。
さて、ここで「150÷30」を計算してしまいそうになりますが、本問ではその計算は間違いです。
まず3×30＝90　と、流速×時間から、流された距離を計算します。つまり、川の流れだけでは、90しか移動できません。　150-90＝60　より、残り60に相当する距離については、漕ぐことで移動しています。つまり、40回漕ぐと60の距離を移動します。
60÷40＝1.5より、1回漕ぐと1.5の距離、移動することが分かります。
問題は、AからBまでの距離を移動するには何回漕げばよいか、ですから、150の距離を移動します。よって
150÷1.5＝100回　です。

(２)

再度確認になりますが、ありがちな間違いとしては、150÷20＝7.5　と、速度を求めるような計算をしてしまうことです。本問の考え方は別になります。
流速を3としているので、3×20＝60　より、流速によって、20秒で60の距離を移動します。よって　150-60＝90　の残りの90の距離を、漕ぐことで移動します。
90÷1.5＝60　より、60回漕ぐと90の距離を移動します。
20秒で60回漕がなくてはならないので、60÷20＝3　より、1秒で3回漕げばよいです。

４

（１）

直方体Aは、たて2㎝、よこ3㎝です。1段目の正方形は、2と3の最小公倍数より、一辺が6㎝の正方形となります。
2㎝×3㎝の長方形を並べて正方形にするときの一辺の長さは、2と3の公倍数になります。つまり、最小公倍数である6の倍数です。よって、1段目が6㎝、2段目が12㎝、3段目が18㎝、4段目が24㎝、5段目が30㎝になります。
よって、30÷2＝15　30÷3＝10　より、15×10＝150個　です。

（２）

まず、立体を上から見たときと下から見たときの表面積を求めます。これは、どちらも　30×30＝900㎠となります。上下なので　900×2＝1800　とします。
次に、縦横の四方から見たときの表面積を考えます。
1段目は、1×6×4、2段目は1×12×4・・・5段目は1×30×4　となります。
よって、1段目から5段目までの和は
1×（6＋12＋18＋24＋30）×4＝360
よって答えは　1800＋360＝2160

５

合否を分けた一題で詳しく解説します

６

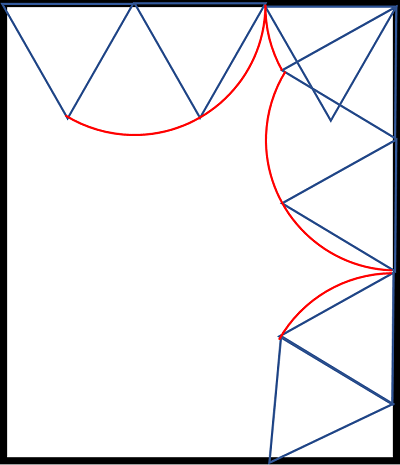
（１）

転がった状況を図にすると、下のようになります。

よって、転がった回数は６回です。

（２）

上の図の赤い線の長さを求めます。直径は全て6×2＝12㎝です。
（6×2）×3.14×（120+30+120+60）/360＝34.54㎝

合否を分けた１題

５

（１）

この問題は、休憩のタイミングについてどのように考えるかがカギとなります。模範解答的な解法とは異なりますが、実際に現場で受験生が取るであろう解法で解説します。少なくとも（１）についてはこちらの方法で解き、（２）で工夫を思いつくことを目指します。
まず、兄と弟が3000mの道のりを進むのに必要な時間を求めます。
兄：3000÷75＝40分
弟：3000÷50＝60分

よって、時間の流れを追うと、次のようになります。

0分	40分	60分	70分	？分
兄弟がスタート	兄がBに到着	兄がBを出発弟がAに到着	弟がAを出発兄はBを出てから10分経過	兄弟が2回目に出会う

弟がAを出発する70分の時点で兄弟が何m離れているかを求め、この距離を二人の速さの和で割ります。
70分の時点では、兄がB地点から10分間進んでいます。よってその距離は、75×10＝750m　この時の兄弟間の距離は　3000-750＝2250m　この250mを、兄弟が向かい合って進み、出会うまでにかかる時間を求めます。　2250÷（75+50）＝18分　よってその時刻は、7：00+70分+18分＝8：28　です。

答え　8：28

（２）

3回目に出会う時間を聞かれているので、（１）で求めた、2回目に出会う時刻から何分後に3回目に出会うかを考えていきます。
さて、二人が反対方向に進み折り返す問題の場合、1回目に出会ってから2回目までに進むまでに2人が進む距離の合計や、2回目に出会ってから3回目に出会うまでに2人が進む距離の合計は、片道2本分になります（イメージde暗記根本原理・実践編061）。
ですから、片道2本分の距離（6000m）を、2人の速さの合計である125で割ればよいのでは？とまず考えます。しかし、この問題の場合は、「休憩」という要素があるために、単純ではありません。
兄は兄で、対岸に到着したら20分休み、弟は弟で対岸に到着したら10分休む。これをそのまま扱ってしまうと、動きが複雑で捉えにくく、計算も煩雑です。
ここで少し工夫を加えます。
兄弟が2回目に出会ってから3回目に出会うまでに、兄弟とも対岸に到着して折り返すので、1回休憩が入ります。もし休憩のタイミングが変わったとしても、兄弟とも1回だけ休憩するのであれば、出会う場所は変わりません。つまり、それぞれAとBに到着した時に休憩するのではなく、2回目に出会った直後に、それぞれ20分と10分休み、それから出発して、A地点とB地点では休憩しないことにしてしまいます。
すると、10分は二人とも一緒に休憩し、次の10分は、兄は休憩、弟だけが進みます。この距離を計算すると
50×10＝500m　を弟が先に一人で進んでいます。
よって、（6000-500）÷（75+50）＝44分
つまり、2回目に出会い、その20分後から数えて44分で3回目に出会います。
よって、8：28+20分+44分＝9：32　となります。

答え　9：32

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？