算数の合否を分けた一題
世田谷学園中学入試対策・算数の合否を分けた一題(2020年度)
難易度分類
| 1 | (1)A (2)A (3)A (4)A (5)B (6)A |
|---|---|
| 2 | (1)C (2)B |
| 3 | (1)B (2)B |
| 4 | (1)A (2)B |
| 5 | (1)A (2)C |
| 6 | (1)B (2)B |
A…世田谷学園合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題
出題総評
図形の移動は昨年に引き続き2年連続で出題されました。平成28年度にも回転体が出ています。図形の動きに関する問題は押さえておくべきでしょう。
また「王道を少し外した旅人算の問題」は例年出題されています。
(2017大問5「等間隔に出るバス」2018大問6「二重円・角度の旅人算」、2019年大問3「カヌーを〇回こぐ」)
いすれも、旅人算・通貨算・流水算のくくりから少し外れたところにある問題です。各塾のテキストには必ず掲載がありますが、しっかりとやりこんでいないと不十分なまま残ってしまうような立ち位置の問題です。旅人算については、こうした細かい論点まで把握しておく必要があります。
立方体以外の立体の切断が過去に出題されたことがあり、2017年の大問6で六角柱の切断が出題されています。今年も大問4で正四面体の切断が出題されました。
この辺りの問題は特徴的かつ複数年度にわたって出題されているので、重点的に学習を行う必要があるでしょう。
問題別寸評
(3)定価を1としたときに、実際に売った値段が0.64であることを利用します。
(4)歩く場合と自転車の場合の速さの比から、時間の比を求め、かかった時間の差を利用します。
距離が一定の場合に、速さの比→時間の比 に変換し、そこから差に着目する流れは定番ですので、本番でも悩まず即答できるように練習しましょう。
(5)A×2+B×1=1470、B×1+C×2=2730 という所から、AとCの差を求めることができます。
2730-1470=1260 より
C×2-A×2=1260
ここから C=A+630 ということが分かります。
この式を
A+B=C に代入します。
A+B=A+630 という所からBが630と分かります。Aは420円です。
この「代入法」は意外と苦手にしている生徒が多い所です。消去算の中でも、代入の考え方を使う問題だけを集めて練習しておくとよいでしょう。
(6)円すいにひもをかける問題です。立体図形にひもをかける問題は、ほぼ全て展開図を書くことで解決します。本問も展開図を書くのですが、その際に、円すいの中心角が90°であることに気づけば、簡単に解くことができたでしょう。
円すいの中心核の公式である 半径/母線=中心角/360 は確実に覚えておきましょう。
サイクリングコース一周の距離を60とおくと分かりやすいでしょう。
1回目にすれ違うのは12分後、以降も12分ごとにすれ違い続けます。
90分ですれ違う回数ですので
90÷12=7あまり6
より、7回です。
列車の長さを【列】とします。列車Aが20秒で進んだ距離は431m+【列】と表せ、また21秒で進んだ距離は717m-【列】と表せます。
このふたつとも速さは同じですので、時間の比がそのまま距離の比になります。つまり距離の比は20:21です。よって
(431+【列】):(717-【列】)=20:21
というところから、内項の積と外項の積が等しいことを利用して解きます。つまり
(431+【列】)×21=(717-【列】)×20
という式を利用します。
もちろん他にも解法はありますが、この「内項の積・外項の積」は適用範囲が広く便利なので、是非覚えておいてください。
「内項の積・外項の積」を使うと、計算の途中で大きな数が登場しやすくなるので、他にスッキリと求める方法をすぐに思いつける場合は、他の方法で解いて構いません。
しかし、他に方法が思いつかなかった場合の最終手段として、いつでも使える状態にしておきましょう。
(1)こちらは単純なつるかめ算です。みかんが4個、りんごが12個です。これが(2)につながります。
(2)
さて、ミカンとリンゴの値段に注目しましょう。みかんは43円、素数です。リンゴは69円、3×23です。つまり、共通の因数を持たないのです。最大公約数は1です。
ということは、ミカンが4個、リンゴが12個の時に合計1000円でしたが、このほかに、ミカンとリンゴを組み合わせて金額をぴったりにできる個数はあるはずがありません。これが方針その1です。
同時に、メロンの金額だけが極端に高いです。メロンの個数で場合分けすることが効率的です。
メロンの個数を1~4で場合分けして、それぞれの場合のミカンとリンゴの個数を考えます。
このように、「因数・約数への感覚」や「どの観点で場合分けするのが正解への近道なのか」といった感覚を鍛えておくことが重要です。
円が頃がった際の軌跡を考える問題です。
こうした問題は、ポイントを押さえた作図ができるかどうかが分かれ道です。
しっかりと作図の手順を覚えましょう。その場その場で考えるのではなく、自分の中で手順を明確化することが大切です。
必須の手順は「動きが変化する瞬間の図形を作図する」ことです。今回の問題でいえば「直線運動から円運動に代わる瞬間」です。円が頂点を乗り越える前後の様子を作図する、と覚えておきましょう。
作図の様子を図で示していきます。
(1)円の中心が動いた長さを求める問題です。

(2)円が通った部分の面積を求める問題です。
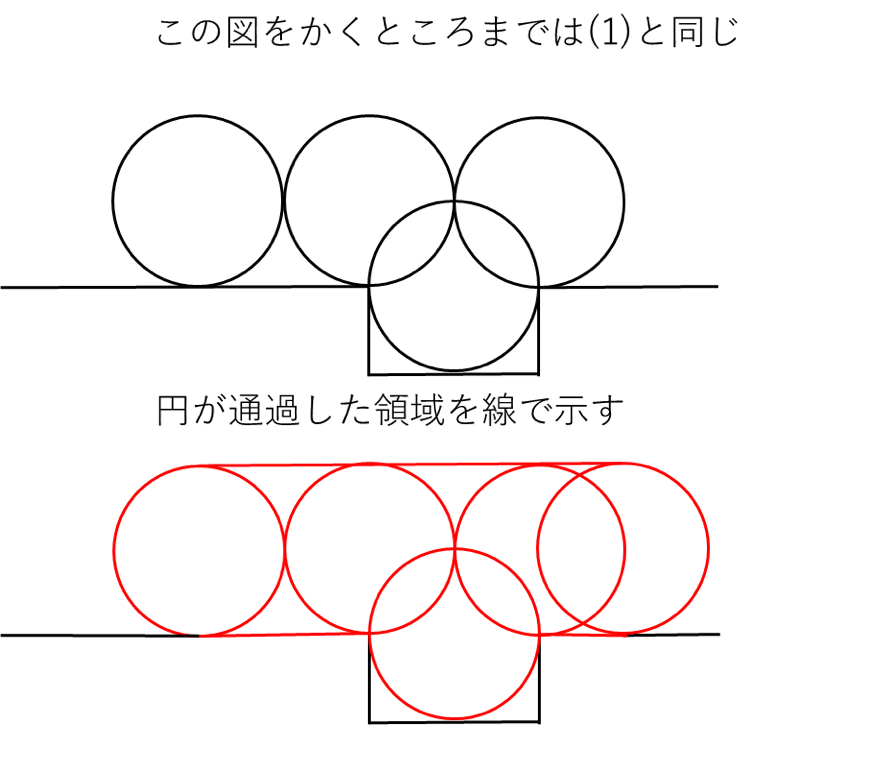
合否を分けた一題
展開図に関する問題です。
最もよく出るのは立方体の展開図ですが、今回は正四面体の角を切り落とした形の展開図です(入試では必要ない知識ですが、切頂四面体といいます)。
この形の展開図は入試で初めて見たという受験生も多かったでしょう。まさかあらゆる立体の展開図を暗記するわけにはいきませんから、根本原理の考え方をしっかり身に着けて、入試の現場で上手に応用できた子が正解できる問題だったでしょう。
根本原理の考え方とは、つまり立方体の展開図です。立方体(サイコロ)の展開図に関する問題は各塾のテキストに必ず掲載があります。そうした問題を通じて、練習することが、所見の問題を攻略する鍵となります。
展開図を展開図のまま処理できるようになりましょう。頭の中で組み立てて考えることは、図形が複雑になればなるほど難しくなります。近年は立方体以外の展開図を出す学校も増えています。
頭の中のイメージに頼らず、展開図をそのまま利用して考える手法を学習しましょう。
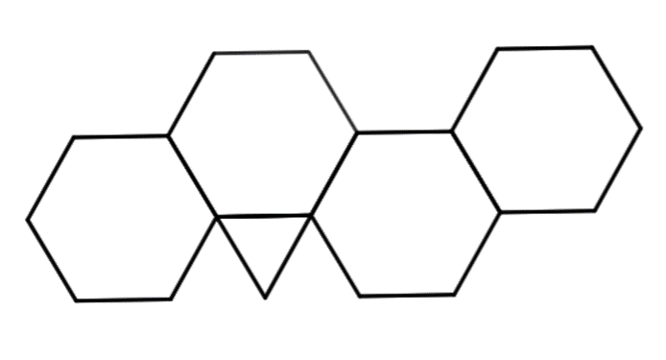
さて、上の図のどこに三角形を足せば良いのでしょうか。
下の図の二つは見えやすかったのではないでしょうか。
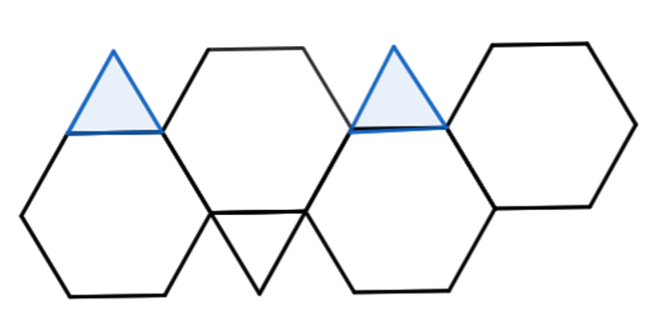
もう一か所の三角形をどこに付け足すかが問題となりますが、ここまでの3つの産気矩形の位置をもう一度見直してみます。
すると、ある規則のようなものが見えるでしょうか?
左の六角形から、上、下、上と付け足されています。ということは、4枚目の六角形の下に付け足されるのでは?という予想がたちます。
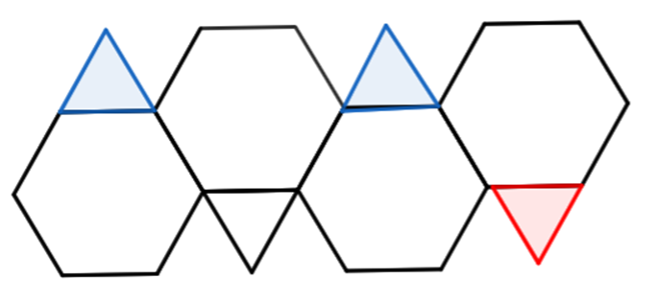
こうして予想がたってしまえば、それが正しいことを確認することはさほど難しくありません。
いくつか可能性・選択肢があるときに、悩んでいるよりは「もしもこれだったらどうだろう?」と試してみるというのは上位行の入試では必要な態度になります。
(2)
出来上がる立体は、以下のような図形です。
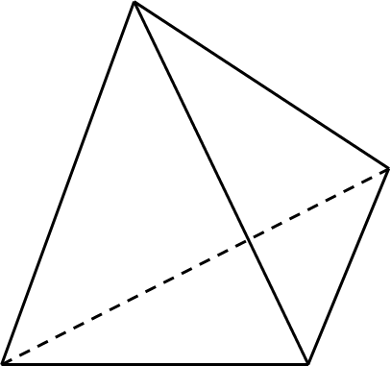
この形の角を切り落として

まとめ
この問題は「展開図」と「立体の切断」、「体積比」という、学習が不十分になりやすい3つの単元を全て複合させて出題されています。
世田谷学園中学の人気は高まっており、テキストで見たことのあるような問題で得点するだけでは合格が難しくなっています。
基本問題の根本原理をきちんと理解していないと解きづらい、ちょうど受験生の差がつく良い問題が出題されています。
闇雲に難問の勉強をする必要はなく、基本問題・典型問題と呼ばれる問題の学習をきちんと行うことが合格への近道です。
しかしただ問題を解けばよいのではなく、その根本原理まで理解することが、ワンランク上の問題で得点できる力の源泉となります。
確実に一歩一歩理解を進め、志望校の合格に近づけましょう。






