算数の合否を分けた一題（2017年度）

算数の合否を分けた一題

本郷入試対策・算数の合否を分けた一題（2017年度）

難易度分類

［１］	（１）A (2)A
［２］	(1)A (2)B (3)A (4)B (5)B (6)C
［３］	(1)A (2)B (3)B
［４］	(1)A (2)A (3)B
［５］	(1)A (2)C

Ａ：本郷中合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、一旦とばすべき問題

問題別寸評

［１］

(1)

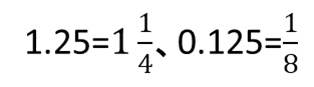
の分数から小数、小数から分数の変換を伴う四則演算の基本。

(2)

分数＋逆算の基本

[2]

(1)

四谷、サピックス、日能研のテキストには必ず出てくる問題なので、受験生であれば皆知っているであろう面積の重なりと割合の問題です。

（2）

相当算。⑤：⑧を利用して全体を１３として計算した方が楽に出てきます。

（3）

ニュートン算の典型パターンです。
増える量を□とすると、
ポンプ1台の時と、3台の時のかかる時間の比が、60分：10分＝６：１
速さの比は、１：６となります。
600－□＝①
1800－□＝⑥より
下の式から上の式を引くと、1200＝⑤、　①＝240Lと求められます。
□＝600－240＝360L・・・これが求めるわきでる量です。
増える量、減る量、はじめの量、この３つを必ず求めることがポイントです。また、時間の比から単位時間当たりどのくらい量が減ったり増えたりしているのかを比で表すようにしましょう。

（4）

ご石の規則性。黒いご石は１、２、３・・・と三角数で並んでいることに気づくことがポイントです。
1組目　○○●
2組目　○○●●
3組目　○○●●●
4組目　○○●●●●

となっています。
初めから数えて160個目がまずどの組に入っているかを求めます。
3+4+5+・・・・・というように、どこまで加えると160に近いか。
（3+15）×13÷2=117
（3+16）×14÷2＝133
（3+17）×15÷2＝150
ということから、
・・・
15組目　○○●●・・・・・・・・・・・●で黒丸が15個並んでいるのが前から数えて150番目です。
160番目は、16組目の10個目なので、2つは白丸が並んでいますが、残り8個は黒丸です。

（１+15）×15÷2＝120　120+8＝128個・・・●の個数

（5）

平均の面積図利用の問題です。

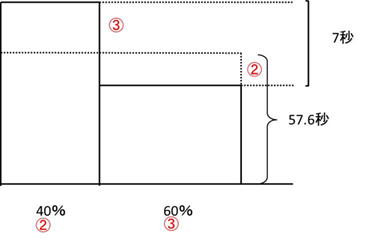
⑤＝７秒
①＝1.4秒
より、②＝1.4×2＝2.8
60％の選手のタイムは、57.6－2.8＝54.8
よって、予選タイムは、
54.8＋3＝57.8秒

（6）

跳ね返りの相似形を探す問題です。
やや数値が難しいですし、相似形がなかなか見つからない場合はこの問題を飛ばして先に進んだ方がよいでしょう。多くの受験生がこの問題に躓いて、点数が伸びなかったのではないかと予想します。

[3]

合否を分けた１題として後述致します。

[4]

特別な三角すい
『イメージde暗記「根本原理」ポイント１６０』の１０８番にある典型問題です。

(1)底面を△AEFとすると、高さが辺BC＝６㎝となります。
（2）底面を△ECFとすると、体積は（１）で求めた９㎤なので、高さを□として式を作って解きます。
（3）立体の回転の問題です。

[5]

コインを１、２、３枚のどれかで交互に取って行き最後に引いた人が負けというゲームは、みなさんどこかでやったことがあるかもしれません。日能研やサピックスの特別授業や思考系の問題を扱う授業では実際に出てきたことがある問題です。

（1）

残っている枚数が１枚の時は、もちろんBの負けになります。
残っている枚数が２枚の時は、Bが１枚取れば、Aの負け。
残っている枚数が３枚の時は、Bが２枚取れば、Aの負け。
残っている枚数が４枚の時は、Bが３枚取れば、Aの負け。
となります。

（2）（1）を踏まえて、
１→３
２→２
３→１
というパターンを考えます。つまり、１枚取ったあとは、３枚取れば合計1＋３＝４
２枚取ったあとは、２枚取れば合計２＋２＝４
３枚取ったあとは、１枚取れば合計３＋１＝４
になり、どれも合計が４です。
また自分が勝つためには、最後にとにかく１枚残せばいいのだから、最後の１枚になる手前が大事。
用意された枚数を□とすると、
□—１が４の倍数のとき、後攻が有利
□—１が４の倍数以外のとき、先攻を選び、先ほどの、足して４になるように取っていけば必ず勝つことができます。

１４−１＝１３なので、１３÷４＝３・・・１
つまりBが先に１枚取ればあとは、足して４になるように取っていけば必ず勝つことができます。

（３）８１−１＝８０で４の倍数となるので、後攻を選択し、足して４になるように取っていけば必ず勝つことができます。

合否を分けた１題

［3］

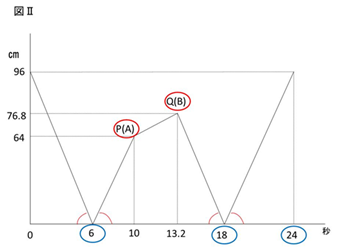
（1）グラフ（図Ⅱ）より、
Qが向きを変えて点Bに戻ったのは、13.2秒後と分かります。
その時に、点Pと点Qの間が76.8㎝離れているので、
点Aと点Pの距離は、96－76.8＝19.2㎝

（2）

グラフにある4つの角度は同じと問題に書いてあるので、
96：64＝3：2より、10÷（3+2）×3＝6秒
また、Pは点Aについたのが、10秒後
そしてまた向きを変えて、13.2-10＝3.2秒で、19.2㎝進んだということがわかるので、
19.2÷3.2=6㎝/秒

（3）

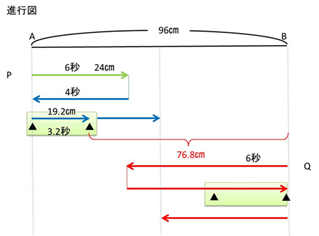
点Qは、1回目に点Pと出会ってから、96-24＝72㎝を4+3.2＝7.2秒で進んでいるということがわかるので　点Qの速さは、72÷7.2＝10㎝/秒
点Qが点Bについて再び向きを変えて動くときは速さは変わらないので、10㎝/秒で進みます。
点Pと点Qは点Qが点Bについたとき、
76.8㎝離れているので、76.8÷（6+10）=4.8秒後に出会います。

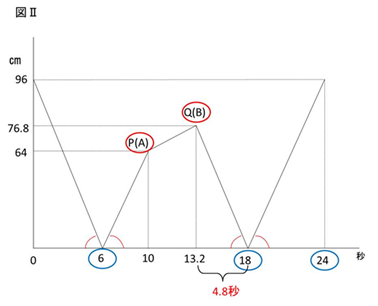
または、図形的にグラフを利用すると、
同じマークのところは同じ角度なので、96：76.8＝5：4
よって、5：4＝6秒：□　　　□＝4.8秒と求めることもできます。

点Qは10㎝/秒で4.8秒進むので、10×4.8=48㎝
これは、96㎝のちょうど半分になります。
そうすると、点Pも48㎝進んでいたとわかります。
2回目に出会ってから、点Pが点Aへ、点Qが点Bに同時に戻ったと問題文に書いてあるので、それぞれ同じ速さということもわかります。
よって、48㎝÷（24-18）＝8㎝/秒

著者：佐々木裕子

この記事は役にたちましたか？