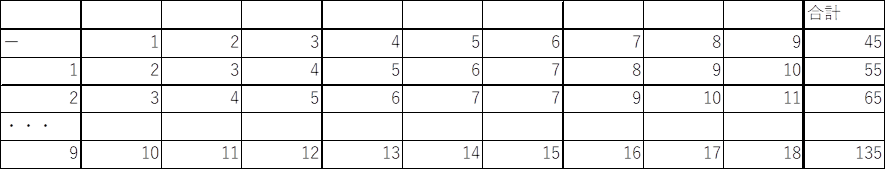算数の合否を分けた一題（2019年度）

算数の合否を分けた一題

本郷入試対策・算数の合否を分けた一題（2019年度）

難易度分類

１	（１）A　（２）A
２	（１）A　（２）A　（３）B　（４）B（５）B　（６）A　（７）A
３	（１）B　（２）B　（３）C
４	（１）A　（２）B
５	（１）B　（２）C　（３）C

A…本郷中合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題

問題別寸評

１

（１）

四則演算の問題。0.125＝1/8などを覚えていると処理時間が短縮できる。

（２）

2019と1346が共に673で割れることが発見できるかがカギとなる。1346が2×673であることから、2019が673の倍数かどうかを確かめてみる、という手順。

２

（１）

上りが9km/時であり、下りが18km/時である。上りと下りの速度の差は、流速の2倍であることを利用する。

（２）

40人の合計点を3.2×40で計算し、そこから2点・3点・5点の生徒の合計点を引いていき、1点と4点の生徒の合計点を求める。そこからつるかめ算に持ち込む。
平均点を見たら合計点を出す、という流れが身についていれば問題なく解けるだろう。

（３）

340円から250円を引くことで、ガム1個、アメ1個、チョコレート1個の値段が求まる。ここから、250－90×2をすることで、アメ1個チョコ2個の値段を求めることが出来る。「アメ1個とチョコ2個の値段」という、見慣れないものの値段を聞かれていることから、どう計算すればよいのか戸惑った受験生もいたかもしれない。
解法の暗記ではなく、その場で設問に応じて考える力が試されている良問。

（４）

図に示されている30cmという長さが、Aから床までの高さの2/5であることを利用する。床からの高さではなく、天井からの高さの数値が与えられているところに新奇性がある。こちらも、きちんと割合の根本原理を理解しているかどうかで差が出る良問。

（５）

3：4：5の直角三角形と相似の三角形を図の中に見つけられるかがポイント。図形の向きが回転しているケースの相似形の発見は苦手とする受験生も多いが、この点をきちんと練習してきたかを問うている。

（６）

和差算を利用して、3つの立方体の一辺の長さを求める問題。立体図形の図に惑わされず、結局は和差算であることに気づけるかがカギとなる。

（７）

正方形が回転した際の点の移動した跡で囲まれた部分の面積を求める問題。正確に計算することが出来れば正解できるでしょう。

３

（１）（２）（３）

「合否を分けた一題」で詳しく解説します。

４

(１)

他校の過去問でも類題が出題されている、近年頻出のテーマ。（１）は易しい問題だが、本問が（２）を考える際のヒントとなっている。

(２)

A君とB君の会話を読むことでヒントを得ていく。B君の発言から、角アと同じ角を探し、また二等辺三角形を利用することが読み取れます。
図のように補助線を引くことで、ア＋イの和は、直角二等辺三角形の角度（45°）と等しいことが分かる。

５

(１)

問題文の意味が読み取れているかを確認する問題。
1回目の1は１番目
2回目の1は10番目
3回目の1は100番目である。

(２)

先頭から100番目までの数を、下の表のようにまとめてみる。

各行の数字を足し合わせると、45,55,65・・・135となることが分かる。
よって、45+55+65+・・・+135+1＝901
が答えとなる。

上の表のように、数を10個ずつ並べるという発想は、問題集に類題が多数収録されている。それらの問題との類似性に気づけるかが正否の鍵となった。

（３）

最初に出る31は4999番目。
以降、5899,5989,5998,6799,6889,6898,6979,6988,6997と続く。よって10番目の数は6997番目である。

合否を分けた１題

３

本郷中学頻出のグラフ問題。面積の差のグラフであり、直観的には、グラフの折れ曲がった地点で、二点PとQがそれぞれどこにいるのかを想像しづらい点に難しさがあります。
グラフ問題の基本通り、線の折れ曲がった点で、傾きが変化した理由が何なのか（例：点Pが点〇に到達したとき、など）を丁寧に把握していくことが必要です。
逆にとらえると、この「変化の理由」が掴めれば、（１）と（２）に関しては解くことが出来るでしょう。

まず各小問に入る前に、グラフの変化している点の原因が何かを特定していきます。
傾きの変化は、点Pと点Qのどちらかが長方形の角に到達したときに起きます。
最初の変化は4秒の地点です。ここは、点PがDに到達した時です。
次の変化は5秒の地点です。ここは、「点QがCに到達した」又は「点PがCに到達した」のどちらかです。そこで、続く部分のグラフを見ると、面積の差が0のまましばらく続いています。この状況になるのは、点PとQがどちらも辺DC上に存在するときです。よって、点イの変化の原因は「点Qが点Cに到達した」だと分かります。
すると、残る2つの変化は、10秒の地点が「点PがCに到達した」で、点線の所（X㎠の地点）が「点Qが点Dに到達した」だと分かります。

以上の情報を図に書き込んでから、各問題を解いていきます。

（１）

グラフより、点PはAを出発してDまでの20cmのみちのりを4秒で進んだことが分かります。よって
20÷4＝5m/秒

答え：毎秒5cm

（２）

グラフより、点Pは4秒から10秒までの6秒間かけて点Dから点Cまで進みます。点Pの速さは5m/秒と（１）で求めましたので
5×6＝30

答え：30cm

（３）

Xの値を求める問題。図のエは、QがDに到達した時です。Xを求めるためには、このとき点Pがどこにいるかを求める必要があります。よって、点QがDに到達するのにかかる時間を求め、そこから点Pの位置を計算します。そのためにまず、点Qの速さから求めていきます。
点QはBからCの20cmのみちのりを5秒間で進んでいますので、Qの秒速は
20÷5＝4m/秒　と分かります。
点Qが点Dに移動するまでには、20＋30＝50cm移動します。これにかかる時間は
50÷4＝12.5秒
次に、この12.5秒の時に点Pがどれだけ進んでいるかを求めます。
12.5×5＝62.5cm
点PはAから出発して62.5cm先にいるので、これは、点CからBに向かって12.5cmの所です。この時の三角形APQの面積は
30×（20-12.5）÷2　であり、三角形AQBの面積は
30×20÷2　です。よって面積の差Xは
30×12.5÷2＝187.5㎠　です。

答え：187.5㎠

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？