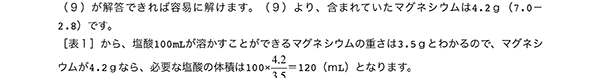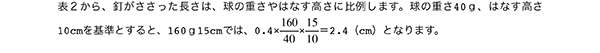理科の合否を分けた一題（2019年度）

理科の合否を分けた一題

浅野中入試対策・理科の合否を分けた一題（2019年度）

難易度分類

１	（１） A　　（２） A　　（３） B　　（４） A　　（５） A　　（６） A （７） A　　（８） B
２	（１） A　　（２） A　　（３） B　　（４）Ａ　　（５） A　　（６） A （７） B　　（８） B　　（９） B　　（10） A
３	（１） A　　（２） A　　（３） A　　（４） A　　（５） B　　（６） B （７） A　　（８） A　　（９） B　　（10） A
４	（１） A　　（２） A　　（３） A　　（４） B　　（５） B　　（６） C

A…浅野合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えればよしとする問題

出題総評

201９年度の浅野は、例年通り基本的知識を問う問題と、少し突っ込んだ知識をきく問題、情報を整理して考えたうえで、数的処理力と計算力が求められる問題が出されています。
題材の取り上げ方に工夫があり、知識のネットワークがどれだけ構築できているか、また、解法の技術がしっかり身についているかをはかるような問題となっています。計算問題のレベルは例年通りですが、全体的に難易度が上がっている印象です。

生物分野の問題は、種子のつくりと遺伝についての問題。
化学分野の問題は、たたら製鉄についての問題。
地学分野の問題は、望遠鏡のしくみと火星大接近についての問題。
物理分野の問題は、斜面を転がる球のする仕事についての問題。

構成としては、大問ごとに前半は知識問題、後半は論理的思考力や数的処理能力を問う問題になっています。前半の知識をしっかり処理したうえで、後半をどこまで戦えるかが合否を分けることになります。

問題構成は、４分野から大問４題、小問40問。
解答形式は、記号選択が25問、数字が12問、言語が３問。昨年あった、グラフがありませんでした。
選択肢は、詳しい知識で「すべてを選ぶ」ものでは、難易度が高くなっています。
数字は、レベルの高い計算問題を含み、出題数は前年並みで時間に照らすと多めです。
言語は出題数が減少し、基本の知識を問うものでした。

問題別寸評

１

（生物）種子のつくりと遺伝についての問題です。
中学で学ぶ遺伝の内容を含みます。文章から読み取ることができますが、基本の考え方を知っているとより有利でした。種子と果実のちがいや、つくりによる分類の知識を、遺伝に絡めて活用できるかどうかがポイントとなります。

（１）

まずは基本知識の確認です。
ひれの形で、メダカのオスとメスとを見分けることができます。

（２）

６個の空欄を12の選択肢から選んでうめていきます。
基本の知識ですが、定まらないところは文脈に注意してあてはめていくようにします。

（３）

本文の「モモの食用部分は子房が変化した場所だからです。」とあります。子房は、母親のからだの一部ですから、母親の遺伝形質が発現し、白桃になります。

（４）

果樹の多くが接ぎ木によって増やされます。
「果樹では地上部分と地下部分は異なる品種となることが一般的で…」とあるところを手がかりにします。

（５）

完全花は、がく・花弁・おしべ・めしべの４つの部分がそろっている花です。
イネは花弁とがくがありませんが、内えい・外えい・護えいがあります。

（６）・（７）

白米はイネの胚乳です。カキも有胚乳種子ですから、種子に胚乳（図のイ）があります。
図のアは果実、ウは子葉、エは胚軸または幼根にあたります。

（８）

本文に「モチ米にウルチ米の花粉がつくと、ウルチ米の性質をしめす米ができてしまう」とあります。胚乳は種子の一部なので、受粉によって父親の形質を受け継ぐからです。したがって、イネと同じように、胚乳を食用とするトウモロコシを選びます。リンゴは花たく、スイカは子房、ジャガイモは地下茎を食用としています。

２

（化学）たたら製鉄に関する問題です。
「砂鉄はなぜさびないのでしょうか？」
だれもがもつ疑問です。この疑問について調べたことがある生徒は、前半はスムーズに取り組めたはずです。後半は、金属の酸化と水溶液との反応についての、難易度が高い計算問題になっています。

（１）

たたら製鉄は、砂鉄や鉄鉱石を木炭といっしょに炉にいれて加熱し酸素を送り込むことで、鉄と二酸化炭素ができる反応を利用しています。砂鉄や鉄鉱石は還元（酸素を離す）反応、木炭は酸化（酸素と結びつく）反応をします。

（２）

鉄の黒さびと赤さびのちがい、マグネシウムや銅を加熱したときの変化についての問題です。これも基本の知識です。

（３）

鉄と砂鉄のちがいについての問題です。砂鉄の正体は、酸化鉄（黒さび）です。さびは、もとの金属の性質を持たないのが一般的ですが、砂鉄の主成分の黒さびは磁鉄鉱ともよばれる磁性体で、磁石につく性質があります。砂鉄を集めるために、磁石を使うのもこのためです。
砂鉄はすでにさびているので、これ以上さびません。したがって、使い捨てカイロに使用することはできません。

（４）

マグネシウムはうすい硫酸と反応して、硫酸マグネシウムになります。このとき水素が発生します。銅は熱伝導がよく焦げつきにくいので、よく鍋やヤカンに利用されます。マグネシウムは加熱すると酸素と激しく反応するため、鍋やヤカンには適しません。

（５）

水素と酸素の性質のちがいについての問題です。基本の知識ですからミスのないように注意します。

（６）

［図１］から、マグネシウム６ｇが燃焼すると10ｇに、銅８ｇが燃焼すると10ｇになることがわかります。金属：酸素：酸化物の重さの比は、マグネシウムが３：２：５、銅が４：１：５ですから、同じ重さの酸素と結びつく金属の重さの比は、マグネシウム：銅＝３：４×２＝３：８です。

（７）

銅は塩酸にとけませんが、酸化銅は塩酸の溶媒の水に溶けることをおさえておきましょう。
この反応で銅と結びついた酸素は0.4ｇ（6.8－6.4）ですから、できた酸化銅は2.0ｇ（0.4×５）なので、酸素と結びつかなかった銅が4.8ｇ（6.8－2.0）残っていることになります。

（８）

塩酸と反応して水素を発生するのはマグネシウムです。
この反応でマグネシウムと結びついた酸素は1.2ｇ（7.6－6.4）ですから、できた酸化マグネシウムは3.0ｇ（1.2×52）です。したがって、酸素と結びつかなかったマグネシウムは4.6ｇ（7.6－3.0）残ります。
［表１］より、十分な量の塩酸があれば、マグネシウムの重さと発生した気体の体積とは比例することがわかるので、マグネシウム4.6ｇがとけると4.6Lの水素が発生することになります。

（９）

（10）

３

（物理）望遠鏡のしくみと火星大接近に関する問題です。
基本の知識→望遠鏡の倍率→公転の計算　の流れになっています。
望遠鏡の倍率については、光の進み方を作図して考えるのが、最もスムーズで確実です。これまで学んできた技術を活用できるかどうかが問われます。

（１）

地球最古の化石とされているのは、現在のところ西オーストラリアで発見された約35億年前のものです。地球誕生は約46億年前、生物誕生は約38憶年前とおぼえておきましょう。

（２）

生命の存在には、液体の水が不可欠です。気体の酸素は、必ずしも必要ではありません。

（３）

写真の天体はリュウグウです。小惑星探査機「はやぶさ２」着地のニュースをおぼえていた生徒が多かったのではないでしょうか。

（４）

対物レンズが結ぶ実像は上下左右逆です。さらにこの実像を接眼レンズによって虚像にすると、実像と同じ向きに見えます。つまり、望遠鏡で見る月は、上下左右逆になっています。

（５）・（６）

→合否を分けた一題参照。

（７）

北極星の高度は、その土地の北緯と同じです。極軸と地表のなす角は、35度にします。

（８）

プレアデス星団はおうし座に見える青白色の星の集まりで、和名を「すばる」といいます。
やや詳しめな知識問題です。

（９）

（10）

太陽と地球の距離を１とすると、火星が最も接近したときの距離は0.5（1.5－1）、最も離れたときは2.5（１＋1.5）となります。したがって、2.5÷0.5＝5（倍）にあたります。

４

（物理）斜面を転がる球のする仕事に関する問題。
球を斜面ではなして転がし、粘土にさした釘やばねに当てる実験です。球の重さや、はなす高さを変えたときのちがいをまとめた表をもとに、規則性を見つけます。

（１）

表２から、水平な面での速さは、はなす高さで決まることがわかります。
はなす高さが10cmなら、球の重さが何ｇであっても、水平な面での速さは140.0（cm/秒）で一定です。

（２）

（３）

（４）

①表２から、球の重さが80ｇのとき、はなす高さが２倍・３倍になると、ばねが縮んだ長さは２倍・３倍より小さい値になります。したがって、ウを選びます。
②表２から、球の重さが40ｇのとき、水平な面での速さが約1.4倍（198.0÷140.0）倍になると、ばねが縮んだ長さも約1.4倍（5.7÷4.0）、水平な面での速さが約1.7倍（242.5÷140.0）になると、ばねが縮んだ長さも約1.7倍（6.9÷4.0）になります。このことから、比例関係にあると考えられるので、アを選びます。

（５）

表２から、球の重さ40ｇ、はなす高さ10cmのとき、ばねは4.0cm縮みます。ばねが縮んだ長さを２倍（8.0÷4.0）にすると、水平な面での速さも２倍になるはずなので、140.0×２＝280（cm/秒）となります。

（６）

1.4×1.4＝1.96≒２、1.7×1.7＝2.89≒３であることに気づけば解答できます。このとき、（４）①のグラフの形がヒントになります。
水平な面での速さが1.4倍のとき、はなす高さは２倍、水平な面での速さが1.7倍のとき、はなす高さは３倍なのですから、水平な面での速さが２倍のとき、はなす高さは４倍（２×２）になります。したがって、10×４＝40（cm）とわかります。

合否を分けた１題

レンズの焦点距離が、望遠鏡の倍率とどのような関係にあるのか、知っている生徒はほとんどいなかったのではないでしょうか。この問題は知っていることをきいているのではなく、解答するために何をどう確認すればよいかを考えて欲しいという意図をふくんでいます。
図３を使って考えることができることに気付き、作図の技術を活かして答えを見つけることができたかどうかが合否を分けたと考え、この問題を取り上げました。

３

（５）

図３を使って、光の進み方から実像がどこにできるかを確かめるために作図をします。
下の図のように、レンズ１の焦点がF１のとき、Pの像はスクリーン上のP１にできます。一方、焦点距離がF1より長いときの実像P２は実像P1より大きくなります。このとき、実像P2は実像P１より遠い位置にできますから、望遠鏡の筒を長くしなければなりません。

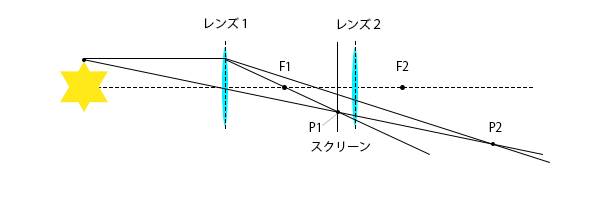
P１：焦点がF1のときのPの実像
P2：焦点距離がF１より大きいときのPの実像

３

（６）

レンズ１によってできた実像P１を、レンズ２を通して見たとき、どこにどのような虚像が見えるかを確かめるために作図をします。
下の図のように、レンズ２の焦点がF２のとき、実像P１の虚像はP1’にできます。また、レンズ２の焦点距離がF2より短いとき、実像P１の虚像はP1”にできます。このとき、虚像P1”は虚像P1’より大きくなります。したがって、対物レンズの焦点距離は大きく、接眼レンズの焦点距離は小さくすると倍率が大きくなるとわかります。

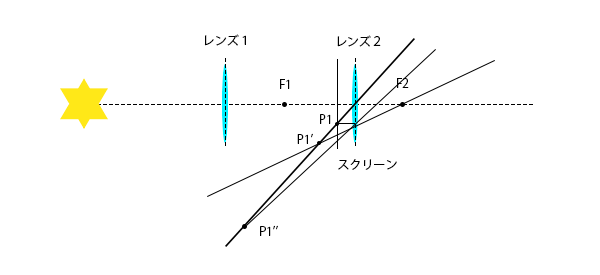
P１’：焦点がF２のときのP１の虚像
P１”：焦点距離がF２より小さいときのP１の虚像