算数の合否を分けた一題
早実中等部入試対策・算数の合否を分けた一題(2016年度)
難易度分類
| 1 | (1)A (2)A (3)A (4)B |
|---|---|
| 2 | (1)①A ②B (2)①A (2)②B |
| 3 | (1)A (2)①B (2)②B |
| 4 | (1)A (2)①A (2)②B |
| 5 | (1)B (2)C (3)C |
A…早稲田実業学校中等部合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題
問題別寸評
(1)
基本的な計算問題です。
1.875=1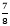 とすぐに分数に変換しましょう。
とすぐに分数に変換しましょう。
(2)
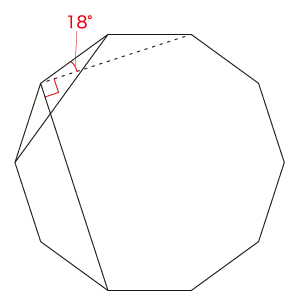
求角の問題です。
様々な解法が考えられますが
図のように補助線を入れて、90°+18°=108°
外角を使って108°+18°=126°が速いでしょう。
(3)
差集め算です。
式で素早く処理してしまいましょう。
生徒の人数を□人とすると
鉛筆・・・6×□+15
ボールペン・・・8×□-2
ボールペンが鉛筆より31本多いので
6×□+15+31=8×□-2
2×□=48
□=24人
6×24+15=159本となります。
(4)
トーナメントの問題ですが、少しひねられた条件設定になっています。
様子がつかめなければ、少ないチームで実験してみるのも良いでしょう。
90校中52校が1回戦、38校が2回戦からの出場となります。
1回戦は52÷2=26試合行われ、26チームが勝ち上がります。
2回戦から出場する38チーム中、26チームは勝ち上がった26チームと対戦、残りの12チームはペアを作り対戦します。
すると、【1回戦勝ち残り】vs【2回戦から参戦】が26試合
【2回戦から参戦】vs【2回戦から参戦】が12÷2=6試合
合計32試合が行われ、32チームが勝ち上がります。
この後も2チームずつペアで対戦してゆくと
3回戦32÷2=16チーム勝ち残り
4回戦16÷2=8チーム勝ち残り
5回戦8÷2=4チーム勝ち残り
6回戦4÷2=2チーム勝ち残り
7回戦2÷2=1チーム優勝
となります。
よって、A校は7勝すれば優勝できることがわかります。
(1)
①
数の性質の有名問題です。決して難しくありませんが、問題文が少し意地悪ですね。
「に」「を」「で」といった助詞に注意してください。かけ算、わり算の順序を間違えないよう、しっかりと設問を読む事!
②
分子が5、10、35、70の4通り
分母が3、6の2通り
よってすべての分数は2×4=8通りとなります。
計算をうまくまとめて処理して下さい。
平面図形と相似の出題です。
設定する数値を工夫することで、計算が楽になります。
沢山三角形があり複雑に見えますが、同じ相似を使えばよいだけですので、実は簡単な出題です。図の中の三角形は全て3:4:5の直角三角形であることを利用して解いてゆきましょう。
最も短い辺BIをまず③と置くと、HI=HG=④
するとEGが分数になってしまいますので、BIを⑨と置きなおします。
BIが⑨、HI=HG=⑫、EG=⑯ あとは数値を埋めてゆくだけです。
ニュートン算の応用問題です。
(1)(2)①は基本解法ですので、得点必須です。
(2)②では立式し、不定方程式に持ち込めたかどうかがポイントです。
最終問は調べ上げです。
非常に時間がかかりますので、よほど腕に自信がない限りは、(1)のみ解いて見直しに時間をさくべきでしょう。
(1)
①
図のように上からみた面をひとつずつ書いて周期を確認します。
2⇒3⇒4⇒1の繰り返しになることがわかります。
②
ひたすら試してゆくしかありませんが、対称性を活用すれば時間を短縮できます。
(2)
2通り考えられますが、いずれも4つの同じ方向への回転が3回と、3つの同じ方向への回転で構成されます。つまり、128にあと1つ数字をたせば、4つの面の和×4となります。
128+□=4の倍数
128は4の倍数ですから、□も4の倍数
□として考えられるのは4、8、12、16・・・
試してゆくと、□=8の時に4つの和が連続する整数となります。
(128+8)÷4=34=7+8+9+10
面ABCの数として考えられるのは7、9、10となります。
合否を分けた一題
本年は早実対策をしっかり積んできた受験生には少し解きづらい出題でした。
早実のお家芸である六角形や、立体図形が出題されなかったことに面食らった受験生もいたでしょう。
難易度として決して高くはありませんが、あっさり解けてしまう解法に気付けたかどうかが合否を分けました。特に大問3の平面図形は相似の本質を問い、形を比較させる良問です。図形に補助線を入れつつも、シンプルに捉えることができれば、あっというまに解くことができます。
(1)
円の問題は、中心から補助線を引いて考えるのが鉄則です。
OからCへ一本線をひけば、OCDとBCDが合同
三角形OBCは正三角形であることがわかります。
三角形ABCが30°60°90°の三角形ですから、辺AB:BC=2:1
BC=16÷2=8cm
補助線が引ければ簡単です。なんとなく60°で解いて正解してしまった受験生もいたのではないでしょうか。
(2)
①
相似の感覚が問われる問題です。
頭を柔らかくして、アとイが相似であることを見抜きましょう。
FD:DB=3:4
面積比は3×3:4×4=9:16となります。
※アとイがなぜ相似かという根拠まで押さえておきましょう。
扇形PDEとOBCが3:4の相似、三角形PEFとOCDも3:4の相似より
扇形PDE-三角形PEF・・・ア、扇形OBC-三角形OCD・・・イ
アとイも3:4の相似比となります。
②
ウを半分に割るとア2つ分になっていることに気付けばおしまいです。
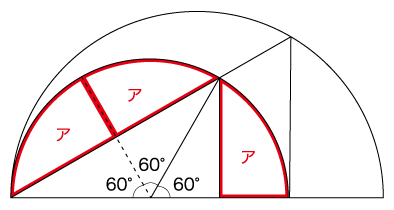
①よりア:イ=9:16
イはアの二倍なので、9×2=18
イ:ウ=16:18=8:9
限られた時間の中で、いかにシンプルに形を見つけることが出来たかが、合否を分けました。
早実中等部入試対策・関連記事一覧
早実中等部入試対策・同じ教科(算数)の記事
早実中等部入試対策・同じテーマ(合否を分けた一題)の記事
- 算数の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2015年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2021年度)
- 算数の合否を分けた一題(2021年度)
- 国語の合否を分けた一題(2021年度)


 (6 投票, 平均値/最大値: 3.67 / 5)
(6 投票, 平均値/最大値: 3.67 / 5)