算数の合否を分けた一題（2021年度）

算数の合否を分けた一題

浦和明の星中入試対策・算数の合否を分けた一題（2021年度）

難易度分類

［１］	(1)　A　　(2)A　　(3)A　　(4)A (5)A (6)B (7)B
［２］	(1)　A　　(2)B
［３］	(1)　A　　(2)B　　(3)B
［４］	(1)　B　　(2)B
［５］	(1)　A　　(2)B　　(3)B

Ａ：浦和明の星合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題→合否を分けた一題
Ｃ：難度・処理量から判断して、得点差がつかない、合否に影響を受けない問題

総評

今年度は、合格者の平均点も昨年より上がり75.3点とやや高めになりました。出題傾向としては特に難度が上がったわけではなく、浦和明の星特有の応用問題だけを解けるということではなく、根本を理解し「考えさせる」良問セットであったと考えます。自分で日ごろから表や図を描いて、1つの解法ではなく、ほかに解き方はないか探求する力の鍛錬が求められています。

問題別寸評

【1】

(1)四則演算の長い式

例年通りの計算問題でした。　約分、通分、繰り上がり、繰り下がりに注意して必ず正答したい問題です。

(2)濃度問題

食塩の濃度問題の基本です。これは解ききりましょう。

(3)過不足算

人数を3倍にするのではなく、配った個数を3倍にして解き進めていきましょう。

(4)通過算

典型問題です。正確に素早く解答を得られるようにしましょう。

(5)円と複合図形の求積

これは正答必須です。半径がわからない円の求積では、半径×半径を正方形から表す典型の問題です。

（6）サイコロ

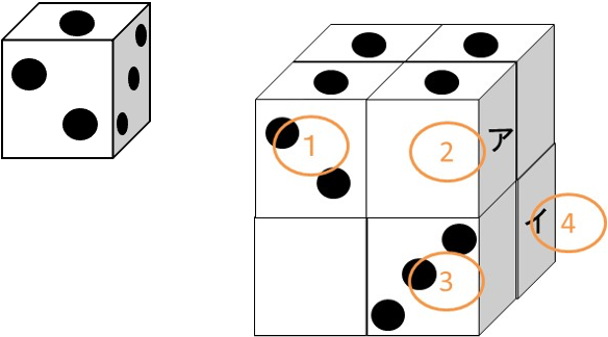
各サイコロに番号を振ります。
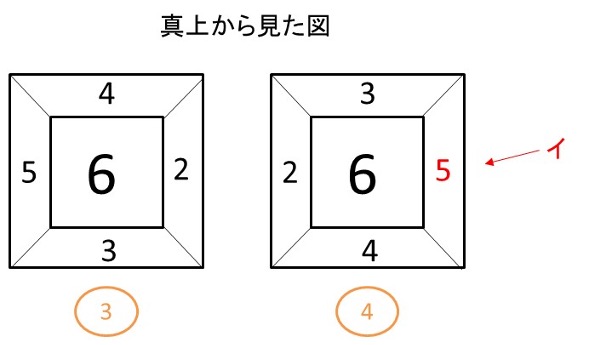
そのサイコロをそれぞれ真上から見た図を次に示します。

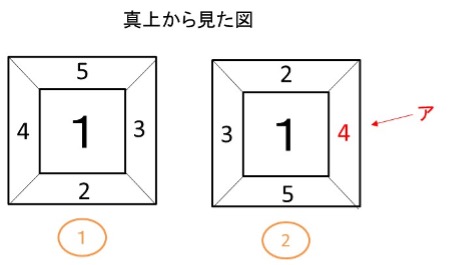
①と②の隣り合ったサイコロを示しています。接している面は同じ数字なので、それを踏まえて
数値を入れていきます。
そうするとア＝４となります。
また、

③と④の隣り合ったサイコロは上図のようになります。
イ＝５となります。

(7)数の性質

条件にある数値を絞り込む問題です。
①一番大きい数は奇数である
②3つの数をすべて足すと31となる
③3つの数から2つずつ取り出して、それぞれ大きい方から小さい方を引いた数を3つ足すと18になる
という3つの条件を利用して解いていきます。
②よりa＋b＋c＝31
ｃ－ｂ
ｂ－a
ｃ－a
の和が(c－a)×2＝18となることに気づくと、ｃ－a＝9となり、
・（a，ｂ，ｃ）＝（8、6、17）→×　　ｂがaより小さくなり条件に合わない
・（a，ｂ，ｃ）＝（6、10、15）→〇
・（a，ｂ，ｃ）＝（4、14、13）→×　　ｂがｃより大きくなり条件に合わない
これ以外は条件にあてはまる整数は存在しないので、答えは、6、10、15となります。
　

【2】仕事算

（1）

典型的な仕事算の問題です。読み違いをしないように正確に読み取り、まずはAとBの仕事の比を求めましょう。
A×12＋B×9＝A×8＋B×12より
A：B＝③：④
③×12＋④×9＝72・・・全体の仕事量
72÷③＝24日

（2）

Cの仕事量を求めます。　72÷36日＝②より、A：B：C＝③：④：②
72÷（③＋④＋②）＝8日

（3）

Aさんが6日間休んだということがわかっているので、⑥で6日間仕事をすると⑥×6日＝36
⑨⑨⑨・・・⑨⑥・・・・・⑥⇒72を終了したので、
72－36＝36
36÷⑨＝4日・・・・3人で働いていた日数となり、4日＋6日＝10日間

これは、基本的な問題になりますので完答すべき問題です。

【3】流水算

（1）

「Aが上流に向かって進む速さとBが下流に向かって進む速さは同じです」という問題文から紐解いていきましょう。
AとBの静水時をそれぞれA、Bとすると、Aの上りはA－36m/分、Bの下りはB＋36m/分です。
それが等しいので、A－36＝B＋36より　A－B＝36＋36＝72が導き出されます。
よって、AとBの静水時の速さの差は72m/分

（2）

静水時での船Aの速さは、
1728÷72＝24分　上りに24分、下りは16分より比がわかります。　　
上り　：　下り
時間の比　24分　：　16分　＝3：2
速さの比　2　：　3
A－36　：　A＋　36　＝　2　：　3
3×（A－36）＝2×（A＋36）　　3×A－108＝2×A＋72より
A＝180m/分

（3）

グラフより

Aの上りとBの下りが等しいということから、40分から72分の間を1：1に時間を比例配分し、
イ町に着いた時間も求めると、相似形が現れるので、
（64－48）：（72－40）＝1：2ということもわかります。
Aの上りは144m/分なので、144×16＝2304m

【4】は合否を分けた一題で取り上げます。

【5】場合の数・不定方程式です。

（1）のりしろが2cmということから、2cmの倍数で一の位が0となるには、
2×5＝10、2×10＝20、2×15＝30・・・などが考えられます。

10cmだけでできるテープの長さは、
ⅰ）2×5とすると、5+1＝6枚であったと考えられるので、
10×6－2×5＝50cm

ⅱ）2×10とすると、10+1=11枚であったと考えられるので、
10×11－2×10＝110－20＝90cm

ⅲ）2×15とすると、15+1＝16枚であるとすると、
10×16－2×15＝160－30＝130cm　しかし、選択肢の中に130cmはないので不適切

よって、答えは、50cm　90cm

（2）最も多い場合は、一番短い10cmを16枚利用する場合です。
10×16枚―2×15＝130cmとなります。

最も少ない場合は、30cmテープと20cmテープ
しかも、のりしろが合っても完成したテープの長さの一の位が0でないといけないので、
それも考えて場合分けします。
テープの数が6枚とすると、
（30cm、20cm）＝（5枚、1枚）か（1枚、5枚）、（4枚、2枚）か（2枚、4枚）の組み合わせとなります。この中で条件に合うのが、（2枚、4枚）です。
30×2＋20×4―2×5＝60＋80－10＝130cmとなります。よって、最も少ない場合は6枚となります。

（3）場合分けをしていきます。
ⅰ）のりしろが5か所だった場合、2×5＝10cmより、
10cmテープ□枚、20cmテープ△枚、30cmテープ〇枚とすると
10×□＋20×△＋30×〇＝130＋10＝140
１，２，３枚の時にこの式は成り立ちます。

ⅱ）のりしろが10か所だった場合、2×10＝20cmより、
10×□＋20×△＋30×〇＝130＋20＝150
８，２，１枚の時にこの式が成り立ちます。

よって、答えは（1，2，3）、（8，2，1）です。

【合否を分けた一題】

【4】

一見簡単そうに見える問題ですが、着眼点を見つけるのにやや時間がかかってしまい、
ポイントが見抜けないと正答にたどり着けない問題だったのではないかと思います。
比の高さから、体積の移り代わりを図に示し、「どこが等しいのか」
「どこが違うのか」ということを見抜く必要があります。
算数の根本的着眼点は、迷ったら、「等しい」部分、「異なる」部分に注目することです。
この問題は、「等しい部分」に注目することに気づかせる良問ではないかと考えます。

図1

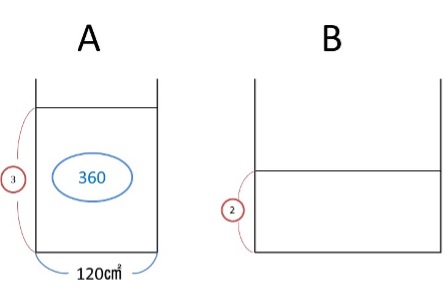
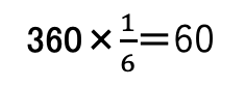がAからBにうつると、
図2

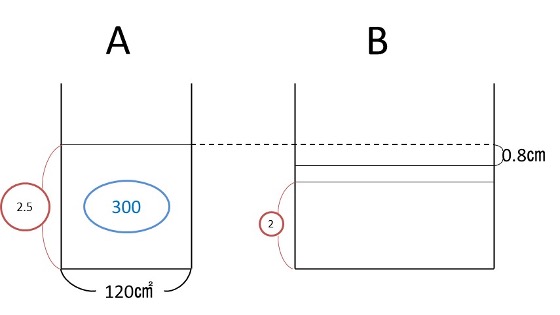
図3

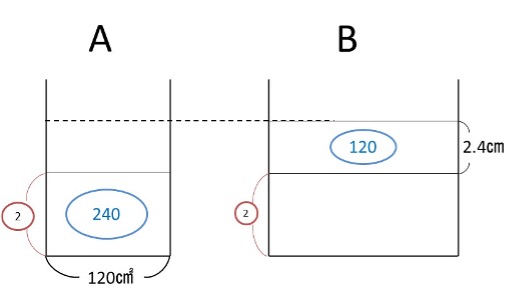
図3より60＋60＝120の体積がAから移ってきたとき、
はじめの②の高さから2.4cm高くなったということに気づくと、この問題はほぼ解けます。
ここが合否の分かれ目ポイントとなるのではないでしょうか。

120で2.4cm高くなるということは、半分の60では、1.2cm高くなっています。
図2より、2.5―2＝1.2＋0.8cmということになり、
0.5＝2cm
1＝4cm
2＝8cm・・・Bのはじめの高さ
3＝12cm・・・Aのはじめの高さ

（2）Aは120㎠×12＝1440㎤の体積が入っていました。

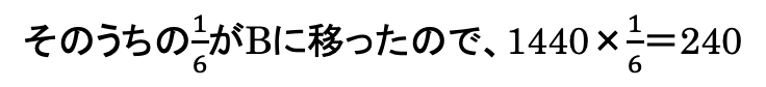
240÷1.2cm＝200㎠・・・Bの底面積
よって、Bには200×８＝1600㎤の水が入っていたことになるので、
（1440＋1600）÷（120＋200）＝9.5cmの深さとなります。
9.5－8＝1.5cm
1.5×120＝180㎤