2013 入試問題 一問一答解説【算数】
【1】 出題総評
立体図形、条件整理、数の性質など、桜蔭算数の頻出テーマは「男子最難関校の入試問題?」と見まがうようなもの。このような、およそ女子校らしからぬテーマからの出題において、かつては解く過程のあらゆる局面で思考力が試されました。しかし、ここ数年、難易度という点では非常に穏やか。確実に易化傾向にあるといえます。2013年度もその流れに沿ったもので、非常に解きやすいセットでした。
2013年度の特徴は以下の3点です。
1. 問題数が少ない
答案用紙から一目瞭然ですが、例年になく問題数が少ないのが今年度の最大の特徴です。
近年の桜蔭算数の傾向のひとつである「処理量が多く、面倒な問題」も配置されていますが、処理速度に不安を抱える受験生でも問題数の少なさに助けられ、時間の圧迫感なく取り組めたようです。
2. 2006年度以来のグラフ作成問題
大問III(1)がグラフ作成問題です。2006年度大問V(2)②水の分散流入問題でグラフ作成が出題されて以来、久々のお目見えでした。
「桜蔭の速さ」はグラフ(ダイヤグラム)主体であり、どの受験生もグラフ(ダイヤグラム)を書いて解く練習を積んできたことでしょう。ただ、この大問IIIは条件がややこしく、読み誤らないように注意しながらグラフを書く必要があり、ここに必要以上に時間をとられないようにしたいところです。
3. 桜蔭志望者にとって「解ける」問題ばかり
目新しい問題がなく、桜蔭対策を積んできた受験生にとって、どれも「解ける問題」だったといえます。解き方の方針が定まらないものはなかったはず。受験生のほとんどが「易しかった」と感想を述べています。1つのミスが命取りになったと思われます。
以上より、2013年度の合否の分かれ目は、1.「桜蔭志望者であれば解ける問題」をミスなく解き切ったか、2.ミスしてしまったときの失点を最小限にとどめる答案作成力が身についていたか、3.現場での時間配分がうまくいったか、です。
処理量の多さや面倒さゆえにミスをしやすい問題という観点から考えると、合否を分けた一題として挙げられるのはI(2)、III、V(3)でしょう。
【2】 出題別難易度
| I | (1)①A ②A (2)B |
|---|---|
| II | A |
| III | (1)B (2)B |
| IV | B |
| V | (1)A (2)A (3)B |
A:桜蔭合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C:難易度や処理量から判断して、部分点狙いで答案を作成すべき問題
【3】 問題別解答・解説
I(1)①②
解答・解説
順算と逆算の計算問題2つ。「面倒」で、どちらもそれなりに「きれいではない数値」になるのは例年通りです。
①の「 ![]() 」は仮分数にせず、帯分数のままで整数部分と分数部分それぞれに3をかけた方が計算量が少なく済みます。
」は仮分数にせず、帯分数のままで整数部分と分数部分それぞれに3をかけた方が計算量が少なく済みます。
②のような途中の□を求める逆算の場合は、自分の答えを□の中に入れて計算し、最後の答えが一致するか(本問の場合は ![]() になるか)確認する検算を心掛けたいところです。
になるか)確認する検算を心掛けたいところです。
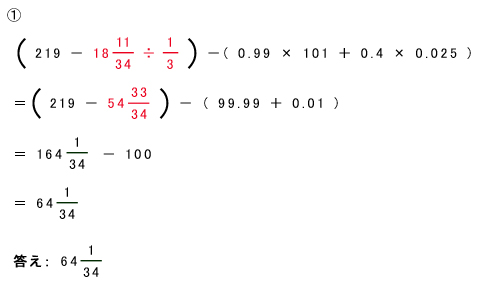

I(2)
解答・解説
周期が絡む仕事の問題。
書き出しの緻密さ、処理の丁寧さが求められる、桜蔭らしい問題です。
30日周期が7セットで、残り585個。ここから後をどれだけ細かく丁寧に処理できたかでしょう。桜蔭志望者にとっては頻出タイプの問題といえ、十分に対策を積んで本番に臨んだ受験生が多かったはずです。
まず、それぞれの周期を考えます。
A : 6日で 25 × 5 = 125個
B : 5日で 30 × 4 = 120個
6日と5日の最小公倍数30日で 125 × ![]() + 120 ×
+ 120 × ![]() = 1345個
= 1345個
10000 ÷ 1345 = 7 あまり585個 より
30日 × 7 = 210日 で残り585個
ここからは丁寧な処理が要求されます。
Aを基準に考えていきましょう。
Aは 6日で 125個
Bは 6日で 120 + 30 = 150個
合わせて 6日で 125 + 150 = 275個
残りは 585 - 275 = 310個
まだまだですね。
よって、6日ではなく12日で考え直してみましょう。
Aは 12日で 125 × 2 = 250個
Bは 12日で 120 × 2 + 30 × 2 = 300個
合わせて 12日で 250 + 300 = 550個
残りは 585 - 550 = 35個
13日目は A・Bともに働くので 35個全て作ることができます。
求める日付は、4月1日から数えて 210 + 13 = 223日目なので
4月1日 + 222日 = 4月223日
223 - ( 30 + 31 + 30 + 31 + 31 + 30 + 31 ) = 9日
よって、 11月9日
求める曜日は
222 ÷ 7 = 31 あまり5日 → 水・木・金・土・日
答え: [ ア ] = 11 [ イ ] = 9 [ ウ ] = 日
II
解答・解説
異なる4つの整数の2数ずつの積から、もとの4つの整数を求める問題。
頭の中で解き方の筋道を立てるのではなく、とりあえず手を動かしてみる習慣がついていれば易しい問題です。
A < B < C < D の条件より
108 = A × B
126 = A × C
162 = A × D または B × C
168 = B × C または A × D
216 = B × D
252 = C × D
ここで、積が最小の 108 = A × B に着目しましょう。
108 = A × Bとなる ( A , B ) の組み合わせを調べます。
ただし、すべてを調べ上げる必要はありません。
Bは2番目に小さい数( A < B < C < D )であることを考えると、それほど大きい数ではないことがわかります。
よって、AとBは近い数どうしの方がよいと判断できます。
( A , B ) = ( 9 , 12 ) ( 6 , 18 ) ( 4 , 27 ) ・・・
( A , B ) = ( 9 , 12 ) のとき
126 = A × C より C = 126 ÷ 9 = 14
216 = B × D より D = 216 ÷ 12 = 18
よって ( A , B , C , D ) = ( 9 , 12 , 14 , 18 )
( A , B ) = ( 6 , 18 ) のとき
126 = A × C より C = 126 ÷ 6 = 21
216 = B × D より D = 216 ÷ 18 = 12
このとき C > D となってしまうので適さない。
答え: A = 9 B = 12 C = 14 D = 18
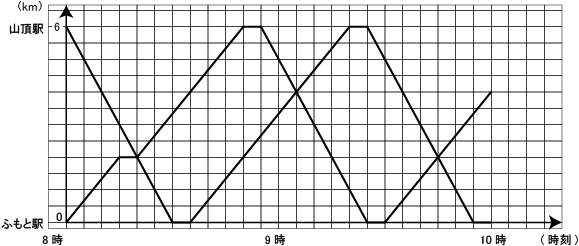
III(1)
解答・解説
2台のケーブルカーが条件に従って往復する様子をグラフ(ダイヤグラム)処理する問題。
グラフ作成問題は2006年度以来ですが、「桜蔭の速さ」はグラフ(ダイヤグラム)主体であり、どの受験生もグラフ(ダイヤグラム)を書く練習を積んできたはず。条件を読み誤らないように注意しながらグラフを書くだけですが、ここに必要以上に時間をとられないようにしたいところです。
ふもと駅寄りのポイントをP、山頂駅寄りのポイントをQとする。
2kmを一区間とすると
上りは 2 ÷ 8 = ![]() 時間 = 15分、 下りは 2 ÷ 12 =
時間 = 15分、 下りは 2 ÷ 12 = ![]() 時間 = 10分
時間 = 10分
■1回目のすれちがい
それぞれ8時に出発し、ポイントPまでAは15分、Bは20分。
よって、1回目のすれちがいは8時20分。Aは5分待つことになります。
※問題文中の「同時にポイントに到着できなかった場合には、どちらかのケーブルカーがどちらかのポイントで待つことになります」という内容を、「ポイントを通過するためには、一方のケーブルカーが来るまで待たなければならない」と誤った認識をした受験生がいたようです。もしそうだとすると、8時に出発してAがポイントP、BがポイントQに着いたあと、2台とも先に進めなくなり、おかしなことになりますね。
■2回目のすれちがい
Aは山頂駅まで30分。5分休憩して、ポイントQまで10分。ポイントQ着は9時5分。
Bはふもと駅着まで10分。5分休憩して、ポイントQまで30分。ポイントQ着は9時5分。
よって、2回目のすれちがいは9時5分。同時に着くので、待ち時間はありません。
■3回目のすれちがい
Aはふもと駅まで20分。5分休憩して、ポイントPまで15分。ポイントP着は9時45分。
Bは山頂駅まで15分。5分休憩して、ポイントPまで20分。ポイントP着は9時45分。
よって、3回目のすれちがいは9時45分。同時に着くので、待ち時間はありません。
■10時まで
AはポイントQまで15分。よって10時にはちょうどポイントQにいます。
Bはふもと駅まで10分。5分休憩。よって10時にはふもと駅にいて、これから出発するところ。
以上の内容をグラフに記入すると、下のようになります。
III(2)
解答・解説
(2)は周期を利用してもよし、グラフをそのまま書き続けてもよし。いずれにしても、(1)で正しくグラフが書けていれば、(2)も得点できます。
ここでは(1)のグラフから周期を読み取って、時刻を求めてみましょう。
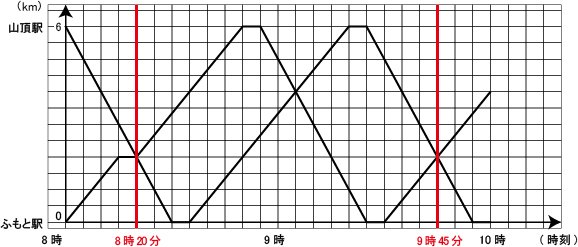
上のグラフより、8時20分から9時45分までの運行の様子が、9時45分以降も繰り返されることがわかります。これを周期とすると
1周期の時間は 9時45分 - 8時20分 = 85分間
3回目のすれちがいが9時45分で、5回目のすれちがいはこのあとちょうどもう1周期したところ。
よって、5回目のすれちがいの時刻は 9時45分 + 85分 = 11時10分
答え: 11時10分
IV
解答・解説
平面図形と比の問題。
長方形のたての比・横の比・面積の比を駆使できるかが問われています。「相似な三角形」や「高さの等しい三角形」といった定番が登場しない平面図形と比の問題なので、足元をすくわれないようにしましょう。
まず、![]() 、
、![]() 、
、![]() について
について
面積比が 3 : 4 : 5 より、 横の長さの比も 3 : 4 : 5
よって、![]() の横の長さは ( 300 - 3 × 2 ) ÷ ( 3 + 4 + 5 ) × 4 = 98m
の横の長さは ( 300 - 3 × 2 ) ÷ ( 3 + 4 + 5 ) × 4 = 98m
次に、(![]() +
+![]() )、(
)、(![]() +
+![]() +
+![]() )について
)について
面積比は ( 1 + 2 ) : ( 3 + 4 + 5 ) = 3 : 12 = 1 : 4
横の長さの比は ( 300 - 3 ) : ( 300 - 3 × 2 ) = 297 : 294 = 99 : 98
よって、たての長さの比は ( 1 ÷ 99 ) : ( 4 ÷ 98 ) = 49 : 198
(![]() +
+![]() +
+![]() )のたての長さは
)のたての長さは
( 250 - 3 ) ÷ ( 49 + 198 ) × 198 = 198m
![]() のたての長さも 198m
のたての長さも 198m
よって、![]() の面積は 198 × 98 = 19404㎠
の面積は 198 × 98 = 19404㎠
答え: 19404㎠
V(1)
解答・解説
底面が台形の四角柱について、体積と表面積を求める問題です。合格のためには絶対に落とせません。
体積
( 30 + 60 ) × 40 ÷ 2 × 30 = 54000㎤
表面積
底面積 × 2 + 側面積
= ( 30 + 60 ) × 40 ÷ 2 × 2 + ( 30 + 40 + 60 + 50 ) × 30
= 9000㎠
答え: 体積 54000㎤ 表面積 9000㎠
V(2)
解答・解説
四角柱から円柱をくりぬいた立体の体積を求める問題です。これも合格のためには確実に得点しなければなりません。
5 × 5 × 3.14 × 40 = 3140㎤ ・・・ 円柱
54000 - 3140 = 50860㎤
答え: 50860㎤
V(3)
解答・解説
2方向からくりぬいたときの表面積を求める問題。トリを飾る問題として、難易度は今一つですが、それなりの処理量があります。AをくりぬいてからBをくりぬくという順番ですが、BをくりぬいてからAをくりぬくと考えた方が、状況をイメージしやすいでしょう。くりぬくことによって「新たに増えた面積」と「なくなった面積」を正確にとらえましょう。
《外側の表面積》
設問(1)で求めた四角柱の表面積から、くりぬいた4つの面( 2つの円、正方形B、正方形Bの向かい側にできた長方形 )の面積を引きます。
正方形Bの面積が面イを12等分したものなので、正方形Bの向かい側にできた長方形の面積も面イの向かい側の面( たて50cm、 横30cmの長方形 )の12等分になります。
9000 - ( 5 × 5 × 3.14 × 2 + 40 × 30 ÷ 12 + 30 × 50 ÷12 )
= 9000 - 382
= 8618㎠
《内側の表面積》
◆正方形Bをくりぬいてできた内側の表面積
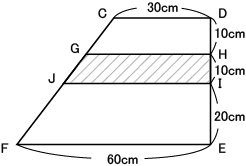
DI=IEより、JIの長さはCDとFEの長さの平均になるので
JI=(30+60)÷2=45cm
同様に、DH=HIより、GHの長さはCDとJIの長さの平均になるので
GH=(30+45)÷2=37.5cm
正方形Bからくりぬいた立体を2個組み合わせると
底面が正方形B、高さ(37.5+45)cmの四角柱となります。
その四角柱の側面積の半分が、正方形Bだけをくりぬいてできた内側の表面積です。
10 × 4 × ( 37.5 + 45 ) ÷ 2 = 1650㎠
ただし、円Aもくりぬいているので、円2つ分の面積が減ります。
よって 1650 - 5 × 5 × 3.14 × 2 = 1493㎠
◆円Aをくりぬいてできた内側の表面積
円柱の側面積のうち、正方形Bをくりぬいた部分を除くと
5 × 2 × 3.14 × ( 40 - 10 ) = 942㎠
以上より、内側の表面積は 1493 + 942 = 2435㎠
よって、内側の表面積と外側の表面積を合わせて 8618 + 2435 = 11053㎠
答え: 11053㎠





