2014 入試問題 一問一答解説【算数】
【1】 出題総評
ここ数年、易化傾向にあった桜蔭の算数。2014年度は相変わらずの易しい問題が並ぶも、最終の大問Vのみ“煩雑さ”という観点から難度が一気に上がりました。
なお、昨年度は問題数を減らしましたが、今年度は従来の問題数に戻っています。
2014年度の特徴は以下の3点です。
1. 軽すぎる1枚目
近年の桜蔭算数の傾向のひとつである「処理量が多く、面倒な問題」は、まず冒頭Iの計算問題のあとに数の性質や規則性の問題として配置されることが多いのですが、今年度はIに配置されていません。
大問IIの長方形の転がり移動は、中学受験を志す生徒であれば何度も解いた経験があるはず。大問IIIの規則性は、設問(2)でジグザグ数列であることを見落とさなければ、桜蔭志望者なら解き切るはず。
桜蔭にしては軽すぎる1枚目、ゆえに1枚目での失点は避けたいところです。
2. 大問Vだけ別次元
軽すぎる1枚目に対して、2枚目はIV(3)、V(3)①②と「処理量が多く、面倒な問題」が配置されています。
特に大問Vは設問(2)、(3)①②と難度が一気に上がり、他の問題と比べてここだけ別次元です。たとえ解き方の方針が定まっても、計算の煩雑さと数値の微妙さに正解の確信が持てないでしょう。
3. ひっかかりやすい設定
I(3):今日の楽器の代金と平日に出直した時の交通費と楽器代を合わせた金額が等しくなるぴったりの定価が求められるので、「低くなる」ために最後に100円をたしたか
大問IV:「重りを10秒後に1個、20秒後に3個、30秒後に5個、40秒後に7個、・・・・・のようにしずめていく」という状況を正しく把握したか(30秒後に沈んでいる重りの個数の合計は5個ではなく、1+3+5=3×3=9個)
大問V(3):「午後5時48分に止まったときには乗客は全員降りている」ので最後の組が乗るのは午後5時28分までと認識できたか、2月11日が祝日であることを考慮できたか
上記のようなひっかかりやすい設定にした問題をちりばめており、正しく解いたつもりでも実は失点している可能性があるといえます。
以上より、2014年度の合否の分かれ目は、1.問題文から設定や条件を注意深く読み取ることができたか、2.軽すぎる1枚目をミスなく短時間で解き切ったか、3.2枚目に集中した処理量が多い問題に粘り強く取り組める根気と計算力を備えていたか、でしょう。
V(3)①②が解けなくても合否に影響なし。それ以外での失点を2問以内におさえれば合格圏内です。
【2】 出題別難易度
| I | (1)①A ②A (2)A (3)B |
|---|---|
| II | (1)A (2)A |
| III | (1)A (2)A |
| IV | (1)A (2)A (3)B |
| V | (1)A (2)B (3)①C ②C |
A:桜蔭合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C:難易度や処理量から判断して、部分点狙いで答案を作成すべき問題
【3】 問題別解答・解説
I(1)①②
解答・解説
①順算、②逆算の計算問題2つ。
工夫が必要な計算問題は例年ほとんど出ませんが、今年度は適宜、分数にせず小数のまま計算することで所要時間を短縮できたはずです。

答え: 0.483
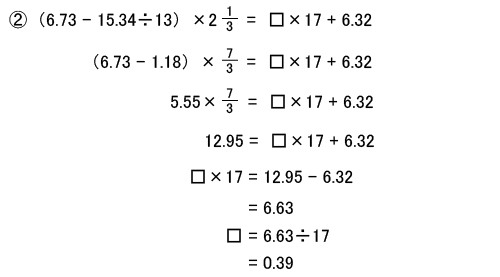
答え: 0.39
I(2)
解答・解説
のりしろありの正方形を並べる問題。
植木算もしくは周期で考えますが、小さい正方形の1辺の長さを8とおけば分数計算に振り回されずに済みます。
小さい正方形の1辺の長さを8とすると、のりしろの長さは1
大きい正方形の1辺の長さは ( 8 - 1 ) × 12 + 1 = 85
小さい正方形の面積 8 × 8
大きい正方形の面積 85 × 85
よって 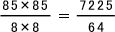
答え: ![]() 倍
倍
I(3)
解答・解説
割合の文章題。
まず、平日は「さらに3割引き」という表現から、定価の8割引きという意味なのか、定価の半額の3割引きという意味なのか、一瞬迷うかもしれませんが後者の意味です。
さらに、前述のように、今日の楽器の代金と平日に出直した時の交通費と楽器代を合わせた金額が等しくなるような定価が19200円なので、「低くなる」ためには100円をたして定価は19300円になります。不等式に馴染みのない小学生にとって、最後にミスをしやすい数値設定になっています。
定価を 100 円とする
今日 100 ÷ 2 = 50
平日 50 × ( 1 - 0.3 ) + ( 250 + 1190 ) × 2 = 35 + 2880
今日の金額より平日の金額が安くなるためには
15 > 2880円
1 > 192円
100 >19200円
よって、定価 100 円は19200円より高いので
19200 + 100 = 19300円以上
答え: 19300円以上
II(1)
解答・解説
長方形の転がり移動。
各塾のテキストの例題レベルであるため、合格のためには絶対に落とせません。
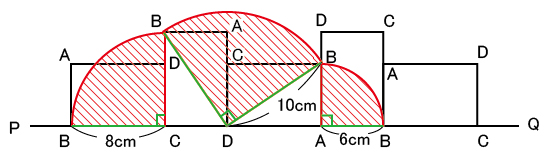
8 × 2 × 3.14 × ![]() + 10 × 2 × 3.14 ×
+ 10 × 2 × 3.14 × ![]() + 6 × 2 × 3.14 ×
+ 6 × 2 × 3.14 × ![]()
= ( 4 + 5 + 3 ) × 3.14
= 12 × 3.14
= 37.68cm
答え: 37.68cm
II(2)
解答・解説
長方形の転がり移動。
設問(1)と同様に、こちらも各塾のテキストの例題レベルであるため、合格のためには絶対に落とせません。2つの直角三角形の足し忘れに注意しましょう。

8 × 8 × 3.14 × ![]() + 10 × 10 × 3.14 ×
+ 10 × 10 × 3.14 × ![]() + 6 × 6 × 3.14 ×
+ 6 × 6 × 3.14 × ![]()
= ( 16 + 25 + 9 ) × 3.14
= 50 × 3.14
= 157㎠
8 × 6 ÷ 2 × 2 = 48㎠
157+48=205㎠
答え: 205㎠
III(1)
解答・解説
規則性の問題。
1,5,9,13,・・・,という1から始まる公差4の等差数列のうち、1~50、151~200に含まれる数の個数を求める問題です。
1~50 ⇒ 1,5,9,・・・,49
1 + 4 × ( □ - 1 ) = 49
= ( 49 - 1 ) ÷ 4 + 1 = 13番目 なので 13個
151~200 ⇒ 153,157,161,・・・,197
1 + 4 × ( □ - 1 ) = 153
= ( 153 - 1 ) ÷ 4 + 1 = 39番目
1 + 4 × ( □ - 1 ) = 197
= ( 197 - 1 ) ÷ 4 + 1 = 50番目
50 - 39 + 1 = 12個
よって 13 + 12 = 25個
答え: 25個
III(2)
解答・解説
規則性の問題。
ジグザグ数列であることを見落とさずに、「前から16番目、左から3番目の児童」が94人目と求めることができたかどうかでしょう。
2列12人ずつの周期で考えると
前から16番目は 16 ÷ 2 = 8周期目の2列目
8周期目の2列目に並んでいる数は
12 × 8 = 96 が左から1番目 ⇒ 96,95,94,93,92,91
左から3番目なので94
94人目は51~100の範囲なので白いぼうし
1,5,9,13,・・・,という数列は「4でわると1余る数」が並んでいるので
94 ÷ 4 = 23 余り2 より 旗は持っていない
答え: 白い帽子をかぶっている 旗は持っていない
IV(1)
解答・解説
今年度の立体図形からの出題はこの大問IV。
切断や展開図、回転体などについて重量級の大問演習を積んできた受験生にとっては拍子抜けするような設問(1)です。
35 × 20 × 1.5 + 30 × 20 × 3.5
= 1050 + 2100
= 3150㎤
答え: 3150㎤
IV(2)
解答・解説
405秒後までに入った水の体積と重りの体積を求め、設問(1)の答えから引けば求められます。
400秒後に79個の重りをしずめているので、405秒後までに全部で
1 + 3 + 5 + ・・・ + 79 = 40 × 40 = 1600個 の重りがしずんでいる
405秒後までに注入した水は
3 × 405 = 1215㎤
よって 3150 - ( 1600 + 1215 ) = 335㎤
答え: 335㎤
IV(3)
解答・解説
設問(2)であと335㎤と求めているので、そこから410秒後、420秒後、430秒後と調べていきましょう。秒単位で分数になるという、桜蔭らしい数値設定です。
| 405秒後 | 410秒後 | 420秒後 | 430秒後 | |
| しずめる重り | 81個 | 83個 | 85個 | |
| 注入する水 | 15㎤ | 30㎤ | 30㎤ | |
| 残り | 335㎤ | 239㎤ | 126㎤ | 11㎤ |
430秒後から、残り11㎤の水を注入するのにかかる時間は 11 ÷ 3 = 3![]() 秒
秒
よって 430 + 3![]() = 433
= 433![]() 秒後
秒後
答え: 433![]() 秒後
秒後
V(1)
解答・解説
観覧車のゴンドラ問題。規則性と速さが絡む大問です。
90組目が他の組と入れかわるのは、Aで乗るときと、一周してAで降りるときの2回あることに注意して下さい。降りるときの154に気付かず、26のみを答えとした受験生がいたことでしょう。
乗るとき 90 - 64 = 26
降りるとき 90 + 64 = 154
答え: 26,154
V(2)
解答・解説
前問を利用して、90組目と入れかわる26組目がBに着くときを考えましょう。大問IV(3)に引き続き、ここでも秒単位で分数になります。
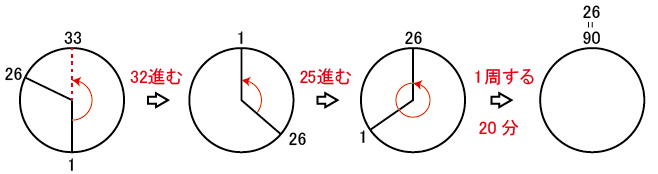
64進むのに20分かかるので、32 + 25 = 57 進むのに
20分 × ![]() = 17
= 17![]() 分 = 17分 48
分 = 17分 48![]() 秒 かかる
秒 かかる
よって 20分 + 17分 48![]() 秒 = 37分48
秒 = 37分48![]() 秒
秒
答え: 37分48![]() 秒後
秒後
V(3)①
解答・解説
「午後5時48分に止まったときには乗客は全員降りている」という条件から、「最後の組が乗るのは午後5時28分まで」という点に注意しましょう。計算が煩雑なうえに、どちらも整数にならないため、不安を抱かせます。
最後の組が乗るのは 17:48 - 20分 = 17:28分 まで
土・日・祝日 17:28-9:00=8時間28分=508分
平日 17:28-10:30=6時間58分=418分
20分で64組が乗るので、1分間で 64 ÷ 20 = 3.2組 が乗る ⇒ 3.2組/分
土・日・祝日 3.2×508=1625.6組が乗るので、1625+1=1626組
平日 3.2×418=1337.6組が乗るので、1337+1=1338組
答え: 土・日・祝日1626組 平日1338組
V(3)②
解答・解説
②は2月11日が祝日であることを忘れずに。
とはいえ、設問(3)にまともに取り組むよりも、その他の見直しに時間を割いて正答率を高める方策をとった受験生が多かったようです。
2月1日 ~ 2月7日 1626 × 2 + 1338 × 5 = 9942組
2月8日 ~ 2月14日 1626 × 3 + 1388 × 4 = 10230組
2月14日までに 9942 + 10230 = 20172組
20172 - 20000 = 172組
2月14日は平日なので 1338 - 172 = 1166組
答え: 2月14日の1166組目





