算数の合否を分けた一題（2020年度）

算数の合否を分けた一題

麻布中入試対策・算数の合否を分けた一題（2020年度）

難易度分類

大問1	A
大問2	(1)A(2)B
大問3	(1)A(2)B
大問4	A
大問5	(1)B(2)B
大問6	(1)A(2)B(3)C(4)C

A：合格を目指すなら必ず得点すべき問題
B：着眼点や解法ツールにより正答率・かかる時間に差がつく問題　⇒　合否を分ける問題
C：難易度や処理量から判断して、得点できなくても合否に影響しない問題

問題別寸評

大問1

比例式の計算です。ほとんどの受験生が正答できたはずですが、解法によって3分程度時間差が生じた問題です。何も考えずに「外項の積＝内項の積」で等式を立てて処理すると、計算が大変なのですが、同じ数を引いても差が変わらない、つまり「差一定」に着目できると素早く求めることができます。
比に関する問題から差一定や和一定に注目させるパターンは麻布の典型といってもよいでしょう。
これからの受験生は意識しておきましょう。

大問2

おうぎ形の求積。
(1)が(2)への誘導になっているかと思いきや、実は関連性はなく、図の中で面積の違いに着目すればよい問題でした。面積の違いを見るうえでポイントになったのは、「対称性」と「補助線」でした。
Dからまっすぐ上にむかって垂直に補助線を引いてウとイを分割することができると、エと切断されたウの左側、オと切断されたイの左側が、それぞれ斜め45度の線を軸とする線対称であることが見えてきます。

大問3

場合の数。
ポイントは「余りによる分類」。そのうえで場合分けして計算するか、樹形図を書いて慎重に取り組むかを選択します。
(1)2で割った余りで分類すると
あまり1→1,3,5
あまり0→2,4,6
同じあまりが隣り合わないためには、0,1,0,1,0,1か、1,0,1,0,1,0と場合分けでき、それぞれのグループのなかで3×2×1＝6通りの入れ替わりがありますので
6×6×2＝72となります。

(2)
計算で取り組むのは危険と判断し、先頭に1を置いた場合の樹形図を描けば難度としては高くない問題でした。
1→2→3→4→5→6
1→6→5→4→2→3
の2通りしかありませんので先頭の6通りにたいしてそれぞれ×2をして12通りとなります。
難度としては高くない2問でしたが、計算だけで済ませようとしてうっかりミスをした受験生もいたでしょう。全てを書き出すと時間がかかりますが、一部分を書いて全体に適応する考え方は必須。
これも対称性の一種ですね。

大問4

麻布の食塩水は仕掛けのある出題もありますが、今年は易しめでした。2通りのてんびんを用いる解法をどこかで経験している受験生がほとんどでしょう。素直に条件を確認すれば思い浮かんだはずで、落とせない問題です。ポイントは「濃さのわからない食塩水2種に対し、2通りの混ぜ方をした場合」、「2通りのてんびんを描き逆比」です。

大問5

合否を分けた一題として後述します。

大問6

問題として一番面白かったのがこの大問6です。
速さ、周期に加えて麻布を攻略するうえで重要な「互いに素」というポイントに気付くことができたかどうかです。距離を置く、角速度を求めるなど様々考えられますが、ふたりの進んだ「距離の和」に着目し、整数で処理できると難度が下がります。
(1)AとBの動く速さが3：5から、同時に地点Pに戻るまでの回転数が、逆比で5：3。
つまり、Aが5回転、Bが3回転して同時に戻ります。
ふたつの点が出会うのは、進んだ距離の和が1周になったときです。ふたつの点は5＋3＝8周しますので、合計8÷1＝8回出会います。地点Pを除いて7回です。
(2)地点P以外で14回すれ違ったということは、AとBの周回数の和が14＋1＝15
ここからAとBの周回数の和分解に入り、
(A,B) ＝ (1,14) (2,13) (3,12) (4,11) (5,10) (6,9) (7,8)の7パターンでてきますが
互いに素であることに着目すると、(3,12) (5,10) (6,9)はもっと早く地点Pで出会ってしまうことになりますので除外。
残るのは、(1,14) (2,13) (4,11) (7,8)の4通りとなります。
(3)（4）ではさらにこの考え方を利用し、AとBの和が2で1回出会うと考えていきます。
麻布らしさの凝縮された難問かつ良問でした。

合否を分けた一題

2020年度の算数は、昨年の大問5つ構成から大問6つ構成に戻りました。
大問毎に難度のばらつきがなく、(1)から(2)にかけて段階を追ってほどよく難度が上昇する構成でした。
冒頭の難易度表のBに該当する部分、特に大問2、大問3のどちらかは(2)まで完答したうえで、大問5できちんと作業できたかどうか、また作業時間を短縮するための工夫ができたかどうかが合否を分けました。

実は今年の麻布の算数には一貫したテーマがあります。
問題別寸評の中でも度々でてきましたが、それは、「対称性」。
大問2、3、5がすべて対称性を発見・利用できると解ける出題でした。

合否を分けた一題では、その中から特に時間差がついたと思われる大問5を扱います。

大問5

麻布のお家芸、正三角形の格子が帰ってきました。
格子を利用した作図問題は頻出で、正方形のものはＨ27,24、正三角形はＨ26,25,23と出題されています。Ｈ30,29では格子の出題自体がありませんでしたので、久しぶりの出題です。
しかしその難度としては易しめ。対称性の利用ができれば、(1)(2)も同じ作業の繰り返しで、正確な作図と、時間を短縮する工夫ができた受験生には解きやすい問題だったでしょう。

まず正確な作図を行うポイントです。
それは、「円が直線と接するとき、接点と中心を結ぶ線は接線と垂直に交わること」の理解です。この理解は円やおうぎ形の回転移動で非常に重要です。

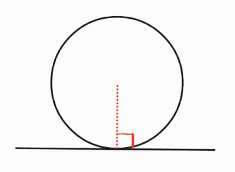
次に、作図の時間を短縮するポイントになったのが、対称性です。
麻布の作図を伴う問題では必須の着眼点です。本問は星型六角形ですので、六等分した一部を調べて6倍することで、時間を短縮することができます。切り分けかたは何通りもありますので、今回は一例を紹介します。
(1)(2)それぞれ下の図のようになります。

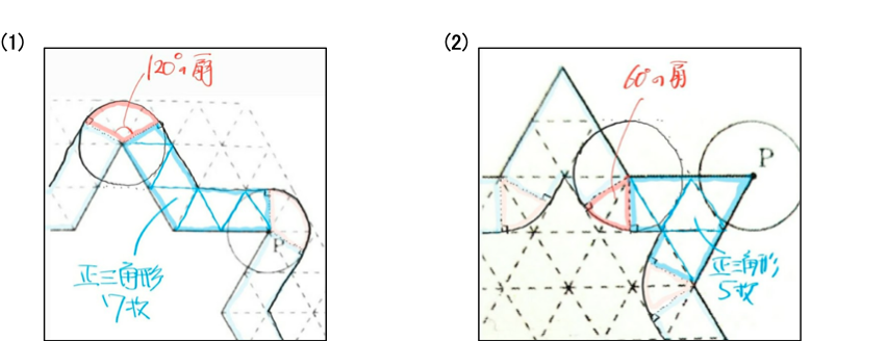
色の濃い青い部分が正三角形で構成されるパーツ、色の濃い赤い部分がおうぎ形のパーツです。
これらをそれぞれ6倍すると答えになります。
(1)は　(正三角形7枚＋120°のおうぎ形)×6＝正三角形42枚＋円×2個
(2)は　(正三角形5枚＋60°のおうぎ形)×6＝正三角形30枚＋円×1個
答え　(1)42×A＋2×B (2)30×A＋1×B

麻布中を目指す受験生は、まず解きやすい問題をしっかり見つけ確実に正解できる基礎力をつけていきましょう。その上でよく出題される「図形問題」や「数を使った調べ問題」に、じっくり時間をかけ丁寧に取り組むようにしていきましょう。過去問を解き進めていけば、麻布中学がよく出題するポイント・着眼点も見えてきます。ぜひ頑張ってください。

著者：吉岡英慈

この記事は役にたちましたか？