算数の合否を分けた一題
麻布中入試対策・算数の合否を分けた一題(2011年度)
麻布中の問題は思考力を要求される問題(A)と典型的な解法で解ける問題(B)のタイプの問題が出題されます。
Bタイプは、麻布中を受験する生徒さんであれば、ほぼ正解を出すことができる問題ばかりです。合否を分けるのはAタイプがどれだけ解けたかによります。
そこで“合否を分けた一題”としては、Bタイプの問題の中で、麻布中学に出題される傾向が高い、条件を見出し、その条件の中で適合する答は何か、を探す、”探索型”の問題を取り上げます。
【2011年 問題3】
計算式 ÷ + ÷ の6ヶ所の空欄に、1,2,3,4,5,6,7,8,9の9個の数字から6個を入れて、計算します。ただし、同じ数字を2ヶ所以上で用いてはいけません。
例
56 ÷ 4 + 3 ÷ 12 = 14 1/4
56 ÷ 1 + 3 ÷ 14 = 8
(1)計算結果が最も大きな整数となるような数字の入れ方を答の欄に書きなさい。
答 ÷ + ÷ _
(2)計算結果が25となるような数字の入れ方をすべて答の欄に書きなさい。
ただし、答の欄はすべて使うとは限りません。
【解説・解答】
(1)について
こういう問題を多くの生徒さんはどのように解くか、というと、適当に数字を入れてみて、解答に近そうなもの見つける、場合が多いです。この“無差別探索”的な解き方によって、SAPIXのBテストで高得点を出している生徒さんもいるようです。
天才的というか、我々講師の立場からすると信じられないのですが、さすがに「カンでとけ!」とは言えませんので(笑)、もう少し論理的に条件を見つけて、数字を入れて、効率的に“探索”する方法を指導します。
○割り算は分数になおすとわかりやすい!
問題文の計算式には割り算が二つあり、各々の商を足して答えを出します。割り算は分数になおすことができますので、この分数がどんな数になるのか、考えてみます。
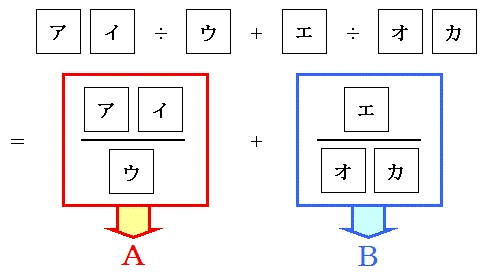
まず、それぞれの□にア~カまでふります。割り算の部分を分数にして、左側をA、右側をBとします。
○AとB、1~9までの整数を入れたらどんな数になるか、考えてみよう!
ここまで、できたら A、B 各々どんな数字になるか考えて見ましょう。
・Aは2桁の数を1桁の数で割る
・Bは1桁の数を2桁の数で割る
わけです。ということは
・AはBより大きい数
・Bは1より小さい数
ということになります(これを見つけるのが“基礎力”です!)。
問題文に戻って、この A+B が最も大きな整数になる場合を考えると、
・Bは1より小さいので、優先的に、できるだけAを大きくする
→ウを小さくする、アイを大きくする
・Bは1より小さい数なので、答が整数であれば、Aは整数にはならない
・残った数を使って、Bをできるだけ大きくする
→オカを小さくし、エを大きくする
ということになります。
この条件にそって、ウをもとにして場合分けをしてみましょう。アイで場合分けをする方法もありますが、2桁ですので、複雑になります。単純なウを場合分けしたほうがわかりやすいのです。
ウはできるだけ小さい数にするのですから、小さい順に“ウ=1の場合”、“ウ=2の場合”・・・と“探索”してみます。
①ウ=1の場合
この場合、Aが整数となってしまって条件に合いません。
②ウ=2の場合
アイを最も大きくします。アイ=98にするとAは整数になりますから、アイ=97になります。
A=97/2=48.5 になり、Bは48.5に足して、整数になる、1より小さい一番大きな数になります。つまり B=0.5 です。
B=0.5 になる数字の組み合わせを考えます。分母は2桁ですから、オカ=12、14、16、18になります。18より大きい数ですと、分子が2桁になってしまい、条件に合いません。
オカ=12の場合、2はすでに使っているので駄目です。オカ=14の場合、7/14=0.5ですが、7はすでに使っているので駄目です。オカ=16の場合、8/16=0.5 でOKです。オカ=18の場合、9/18=0.5 になり、9はすでに使っています。
つまり、オカ=16 エ=8になります。
③ウ=3の場合
A=97/3=32.33・・となってしまい、②ウ=2の場合と比べて小さくなってしまいますので、これは条件に合いません。ウをさらに大きくするともっと数は小さくなってしまいます。よって答は次のようになります。
答 97 ÷ 2 + 8 ÷ 16
(2)について
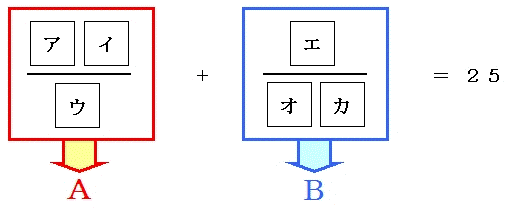
(1)と同様に下の図のようにして、A、Bそれぞれどんな数になるのか考えて見ましょう。
Bは(1)に書いたように“1より小さい数”です。 つまり、Aは “24より大きく25より小さい数” になります。
(2)もウをもとに場合分けをしてみましょう。
①ウ=1の場合
これはAが整数になってしまい、条件に合いません。
②ウ=2の場合
アイは2で割ると24より大きく25より小さい数ですから、 アイ=49 になります。A=49/2=24.5 この時、B=1/2=8/16 になります。
③ウ=3の場合
アイ=74です。A=74/3=24.666・・ この時、B=1/3=6/18 になります。
④ウ=4の場合
アイ=97 或いは 98です。 アイ=97の時、A=97/4=24.25 この時、B=3/4=9/12、12/16・・・で条件に合いません。
アイ=98の時、A=98/4=24.5 この時、B=1/2=6/12 になります。
⑤ウ=5の場合
アイは 24×5=100 から 25×5=125 の間の数となってしまい、3桁ですから条件に合いません。ウ=6以上になると、アイはさらに大きい数になりますから、条件に合いません。
よって、答はウ=2~4の場合の3通りになります。
答
49 ÷ 2 + 8 ÷ 16
74 ÷ 2 + 8 ÷ 16
98 ÷ 4 + 6 ÷ 12
このように、やみくもに数字を入れるのではなく、わかりやすい式にかえて(今回は割り算を分数にかえて)、各々どんな数になるか、条件を出して、一番わかりやすい数で場合分けをして考えると、難易度は確かに高いですが、解けない問題ではないのです。
問題のタイプとしては頻出ですので、このような解き方、思考は慣れておくと良いでしょう。
麻布中入試対策・関連記事一覧
麻布中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 時期による算数の学習法の提案(概要)
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 塾ごとの算数の学習法の提案(日能研生)
- 算数担当講師から麻布中学入学を目指す皆さんへアドバイス
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
麻布中入試対策・同じテーマ(合否を分けた一題)の記事
- 社会の合否を分けた一題(2010年度)
- 国語の合否を分けた一題(2011年度)
- 理科の合否を分けた一題(2010年度)
- 社会の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 国語の合否を分けた一題(2013年度)
- 理科の合否を分けた一題(2013年度)
- 社会の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)
- 算数の合否を分けた一題(2021年度)

 (10 投票, 平均値/最大値: 4.20 / 5)
(10 投票, 平均値/最大値: 4.20 / 5)




