算数の合否を分けた一題（2018年度）

算数の合否を分けた一題

駒東中入試対策・算数の合否を分けた一題（2018年度）

難易度分類

[１]	(1) Ａ　　(2) Ａ　　(3) A　　(4) Ｂ
[２]	(1) ① Ａ　 ② Ａ　　(2) ① Ａ　 ② Ａ　　(3) Ｃ
[３]	(1) Ａ　　(2) Ａ　　(3) Ｂ　　(4) Ｃ
[４]	(1) A　　(2) Ｂ　　(3) 数値Ｃ　具体例Ｂ

A…駒場東邦中学合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題

出題総評

全体的には、やや難度を抑えた出題だったと言えます。今年、特筆すべきポイントは２つありました。1つ目は、昨年話題となり、今後も続くのかが注目された記述問題が出題されなかったこと、2つ目は、平成27年度以来となるパズル系の数え上げ問題が出題されたことです。

問題別寸評

１

(1)～(3)は、極めて基本的な計算問題と小問集合でした。ここは確実に得点しておきたいところです。 (4)は、約数を使用した解法を知っていたかどうかで差が出る問題だったかもしれません。

（１）

消費税の処理で端数が出るわけでもなく、ごくごく基本的な割合の問題でした。確実に正解してください。

（２）

入試年度が答えの数字になる問題が２年続いていましたが、今年は問題の中に2018が登場する形になりました。2018は、2×1009にしか素因数分解できない数字ですから、約分しようにもなかなかできず、もどかしい思いをしたかもしれません。分子を計算するとき、すべて掛け合わせずに、上手に共通する数字をみつけてかっこでくくるようにすると良いでしょう。

（３）

もちろん、重なりの部分を考えなければなりませんが、駒東を受験した方であれば、何度も取り組んできたタイプの問題だったと思います。円すい台を２つつなげた形になりますが、高さも３の倍数ですので、比較的楽に計算できます。

（４）

古代エジプトでは、ほぼすべての分数を単位分数の和で表していたため、一部では「エジプト算」などという名前もつけられている典型問題です。しかし、様々な単位分数を引いた答えも単位分数になるような組み合わせをひたすら探す解法では、なかなか４つ探し出すことはできないでしょう。与えられた分数を倍分（約分の逆の作業）して様々な形をつくり、約数を使用して探すとスムーズに解けます。
本問を「合否を分けた一題」として、あとで詳しく説明します。

２

大問[２]は立体図形ですが、例年のような難しいものではなく、全体的に易問でした。(1)も複数回の切断ではありませんし、切り方自体想像しやすいので、簡単に解けたはずです。(3)は少し難しく感じますが、適切な着眼点を持つことができれば、急に易しい問題に変わります。

（１）

切断面が等脚台形になることは、容易に想像できたと思います。
底面以外の切り口は１辺3cmの正三角形の１辺となりますし、残りの１辺も底面の正方形の１辺に等しくなるので、周の長さも暗算で求まります。

（２）

長さ6cmの糸の先端が動ける範囲ですから、基本的には半径6cmの円になります。
もちろん、動く場所が立体図形の表面上なので単純な円にはなりませんが、解答用紙で与えられた展開図を利用して考えれば、半径6cm・中心角60度のおうぎ形４つ分になることがすぐに分かったと思います。与えられた数字も計算しやすく、サービス問題と言えるかもしれません。

（３）

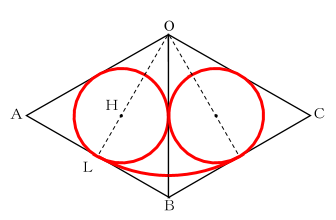
棒を立てた点が正三角形の重心であることを知らなくても、正三角形の対称性に気づけば、OLがABと垂直に交わり、正三角形OABの対称軸になることが容易に分かると思います。また、問題文中のヒントから、OH：HL＝２：１になることも分かりますから、半径１の円周２つ分と、半径3で中心角60度のおうぎ形の弧の長さの和が、糸の先端が描く図形の長さの総和となります。
なお、棒の太さは考えませんから、棒に意図が絡まった状態でグルグル回っても、この円の上を動き続けることになります。

３

同じ数字をいくつも掛け合わせた時の「一の位」の数字という問題はよく見かけますが、「十の位」を扱った問題は珍しいです。
しかし、実際に2018個掛け合わせることを求められているはずはありませんから、何かしら規則性が見つかるであろうことはすぐに見当がついたでしょう。

（１）

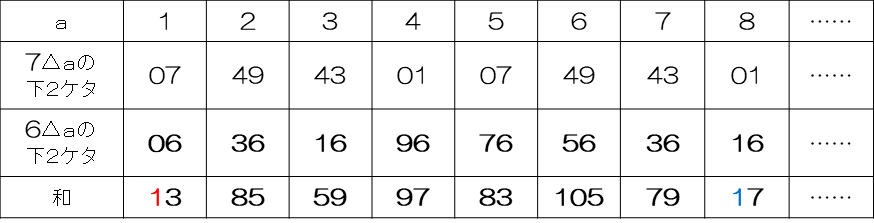
この(1)は、(2)・(4)に向けての誘導問題ですから、ケアレスミスさえ気をつければ、問題自体は易しかったはずです。下2ケタだけを見ながら、実際に計算をして規則性を探しましょう。
7×7＝49　→　49×7＝～43　→　～43×7＝～01　→　……　　　すると

となります。

（２）

(1)で発見した規則性（周期算）を利用して2018番目の数を求めるだけですから、暗算でも出せるくらい易しい問題です。
ケアレスミスに気を付けて、確実に得点しておきましょう。

（３）

７に場合に比べると規則性が見つけにくいですが、やはり2018番目を探すのですから、規則性が現れないはずがありません。絶対に周期ができるはずだという強い気持ちをもって探しましょう。
実際に計算してみると、下2ケタが次のようになります。

お気づきでしょうか。答えが１ケタしかなかった最初だけは例外となりますが、それ以外は５→３→１→９→７の５個が１周期となっています。

（４）

この問題で正解を導き出すには、とても丁寧な作業が必要となります。そのため、おそらく実際の入試では、一旦後回しにしておいて、残り時間の中で取り組むことになるでしょう。
その意味では、解ければ合格を大きく引き寄せることになりますが、ここで合否が分かれるという問題ではありません。
しかし、非常に面白い問題ですので、少し解説をしておきます。
(1)～(3)で誘導された通り、（7△a）の値は4個周期、（6△a）の値は5個周期、で変化しています。したがって、最小公倍数である20個を書き出して考えることになります。
ここで注意しなければならないのは、繰り上がりがあるために、十の位だけで考えるわけにはいかないということです。下2ケタの周期を書き出して合計を求め、十の位が１になるものを探します。

このように、１周期あたり２つ、十の位が１になるものが存在することになります。
2018を20ずつの周期に分けると、
　2018÷20＝100あまり18
ここで、あまり18の中には、十の位が１になるタイミングが２回とも含まれますので、
　2×100＋2＝202（通り）　となります。
さて、ここで油断して、解答欄に「202」と書いてしまわないように注意してください。
(3)で確認した通り、最初だけは周期が崩れていました。この、最初の部分を見てみると……

何と、最初の例外部分が、まさに「十の位が１になる」ところだったのです。
したがって、正解は203通りです。
１周期20個の和をミスなく求め、さらにこの最初の罠にも気づかないと得点になりませんので、時間が掛かる割に正答率の低い問題だったはずです。

４

問題を読んだ瞬間に、「あっ、ビンゴだ！」と思ったのではないでしょうか。中央のマスが初めから塗られているというあたりも、ビンゴの要素を取り入れているのが分かります。
楽しそうなのでつい手を出したくなってしまいますが、わざわざ作業用の図を与えているような問題が、短時間で解けるはずはありません。
途中式を評価してもらえるならまだしも、すべて探しきらないと得点にならないというリスクを考えると、(3)には深入りしない方が得策だと思います。

（１）

４回の作業で「終わり」となるためには、初めから塗られている中央のマスを使い、ストレートで１列塗り終わる必要があります。数字の順は関係なく、あくまで「組み合わせ」ですので、中央縦・中央横・ななめ２列の４通りしかありません。

（２）

５回の作業で「終わり」となるためには、中央のマスを使わずにストレートで５個塗るか、中央のマスを使いつつ１個だけ関係のないところを塗るかのいずれかです。
中央のマスを使わない列は、縦に４列、横に４列の合計８列です。
中央のマスを使う塗り方を１列作ると、関係ないマスがそれぞれ20ヶ所ずつ存在しますから、(1)の４列がすべて20通りずつあることになります。

（３）

作業を19回繰り返したということは、初めから塗ってある中央のマスを含めて20個のマスが塗られていることになります。それでも「終わり」とならないためには、縦・横・ななめすべての列に、どこか１ヶ所は塗られていないマスが存在しなければなりません。
塗られていない５個のマスで、縦５列・横５列のすべてに散りばめなければならないので、同じ列に塗られていないマスが重ならないように配置していきます。
つまり、塗られていないマスの位置に注目して調べ上げていくことになります。

合否を分けた一題