算数の合否を分けた一題（2020年度）

難易度分類

[１]	(1) Ａ　　(2) Ａ　　(3) Ａ　　(4) ① Ａ　 ② Ｂ
[２]	(1) Ａ　　(2) Ｂ
[３]	(1) Ａ　　(2) Ａ　　(3) Ｃ
[４]	(1) Ａ　　(2) Ａ　　(3) Ｃ

A…駒場東邦中学合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題

出題総評

昨年度の入試で例年より５問前後減少した小問数が、今年もほぼ引き継がれる形となりました。以前より、一題に掛かる時間が増えたということなのかもしれません。
また、昨年の立体図形の見取り図を描かせる問題に対して、今年は平面図形の回転移動の軌跡を描かせる問題がありました。いずれも易しい問題のはずですが、普段から自分で図を描く習慣のない人には、コンパスがうまく使えないなど、意外と時間がかかる問題だったかもしれません。
さらに、こちらも恒例となっている「西暦の数字（2020）」を使う問題や、オリンピックのマークを意識したような五つの輪の問題、陸上トラックの問題など、今年も駒場東邦らしい、遊び心満載の入試問題でした。
論理・推理系の問題が２題も出ていたことも、今年度の一つの特徴だったかもしれません。

問題別寸評

１

(1)～(3)は、極めて基本的な計算問題と一行問題でした。ここは確実に正解しておきたいところです。 (4)は、論理思考と丁寧な調べ上げが必要な問題で、この手の問題に慣れているかどうかで解答時間に差が出た可能性があります。

（１）

0.375や2.25などの小数は、すぐ分数に直せるように覚えておきましょう。計算の順序にさえ気をつければけっして難しくはありませんので、確実に正解してください。

（２）

正三角形が転がる様子をしっかり想像して、ミスのないように作図しましょう。半周したところでスタートと同じ状態になるという対称性を利用できると、より簡単になります。

（３）

（BD×BP）：（BE×BQ）＝１：２、（BE×BC）：（BQ×BA）＝２：３という性質を使用する、辺の比と面積比に関する基本問題です。確実に正解してください。

（４）

①は、「各円ごとの５つの数の合計が40」という条件を使って、左側から順に２つずつの数の和を求めていくだけの単純な問題です。つまり、一番左の円にある５つの数字の和が40になるためには、A＋B＝14でなければなりません。そうすると、左から２番目の円の上にある５つの数字の和を40にするためには、C＋D＝9……というように、連鎖的に、E＋F＝16、G＋H＝8、I＋J＝24と求まります。
②では、先ほど求めた２つずつの数の和を利用して、実際に入る数の候補を絞っていきます。その際、使われていない数字が一目で分かるように、まずは１から17までの数字を書き並べて、すでに出ている数字を消し込みましょう。面倒なようで、これが一番効果的な条件整理となります。

２

大問[２]は、毎年のように出題される「数の性質」に関する問題です。また、駒東の大好きな「西暦の数字」を使った問題でもありました。
(1)は、問題の意味を確認しているだけなので簡単です。ミスをしないように確実に解きましょう。
(2)は、無数にある答えの中の一例を示せばよい問題なのですが、がむしゃらに探してもなかなか見つかりません。解法によってかかる時間に差が出ますので、これを今年の「合否を分けた一題」としたいと思います。

（１）

＜1÷101＞は、1÷101＝0.00990099……となりますので、「００９９」の４つで１周期となります。もちろん、2020は４で割り切れる数ですので、答えは「９」となります。
＜40÷2020＞は、40÷2020が2÷101と等しいことを利用しましょう。つまり、
40÷2020＝2÷101＝1÷101×2＝0.00990099……×2＝0.01980198……
と計算できますので、小数第2020位の数字は「８」です。

（２）

本問を「合否を分けた一題」とし、詳しくは後述します。

３

易しい(1)や(2)を解きつつ、「もしかしたらオリンピックを意識した出題かな……」などと考えて気を抜くと、(3)では思わぬ形で足元をすくわれてしまいます。
実際の入試では、割と時間が掛かるために後回しにしたという人が多いでしょうから、この(3)が直接合否に響くことは少ないと思いますが、たっぷり時間を掛けた上でミスをしてしまうと、致命傷になりかねない問題でした。

（１）

円の直径と円周率3.14が与えられていますから、曲線部分の長さは円周の公式を使って求めます。
そうなると、図の太線部分が200ｍと決まっていますので、残りが直線部分（AD＋BC）です。最後に２で割るのを忘れないようにしましょう。
（200－40×3.14）÷2＝37.2（ｍ）

（２）

どのコースでも直線部分の長さは一緒ですから、１周の長さを等しくするためには、曲線部分が増えてしまう分だけスタート地点を前にずらす必要があります。
１つ外側のコースになるたびに、直径が２ｍずつ長くなりますから、円周全体（左右の曲線部分の合計）では 2×3.14＝6.28（ｍ）長くなります。
つまり、２コースを走る選手は１コースを走る選手より6.28ｍ前方からスタートすることになります。

（３）

200ｍ競争を行うので、１コースの選手はちょうど１周走ればよいのですが、２コースの選手は、スタート地点を前にずらした分だけ、直線部分の長さが減り、曲線部分の長さが増えることになります。
そして、(2)の結果は、１コースと２コースの間だけでなく、２コースと３コース、３コースと４コースなど、隣り合うすべてのコースで成立するはずなのですが……ここで気をつけなければならないのが、(1)で求めたBCの長さです。点SはBCの中間ですから、SC間の長さは18.6ｍしかありません。
その結果、３コースのじろう君は、１コースのたろう君より6.28×2＝12.56ｍ前からスタートするだけでよいので、SC間の直線部分の範囲内に納まるのですが、６コースのさぶろう君は１コースのたろう君より6.28×5＝31.4ｍ前からスタートしなければならず、18.6ｍしかない直前部分をこえてしまうのです。つまり、直線部分の減少は18.6ｍ分しか起こりません。
この結果、３人が走る直線部分と曲線部分の長さを比べると、次のようになります。

これに対して、３人の速さの比は、たろう君の速さを１とすると

となりますから、距離を速さの比で割って時間の比を求めると（※小数第３位を四捨五入しています）

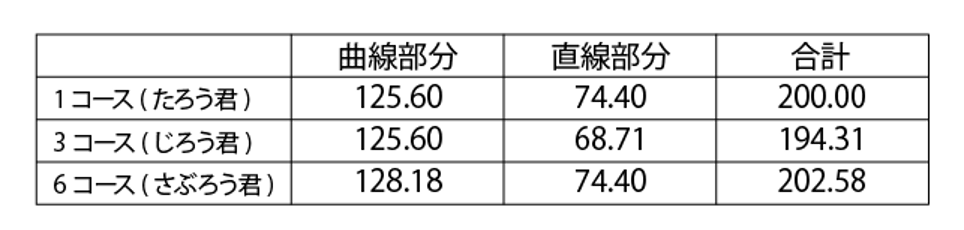
したがって、１位はじろう君、２位はたろう君、３位はさぶろう君となります。

４

パズル好きな人の挑戦心に火をつけるような、論理思考の問題です。
しかし、制限時間のあるテスト中に解かなければならないわけですから、いかにシンプルに、効率よく考えられるかがポイントとなります。

（１）

当然のことながら、一番上に置いた紙（ア）だけは、他の紙に隠される部分がありませんから、もともとの長方形の面積が「見えている部分の面積」となります。４色すべての「見えている部分」の面積が等しかったことから、もともとの面積が一番小さい青い紙が（ア）、等しい面積は144㎠と分かります。
そうなると、４色とも144㎠ずつ見えているわけですから、正方形全体の面積はその４倍ということになります。
　144×4＝（2×2×2×2×3×3）×（2×2）
＝（2×2×2×3）×（2×2×2×3）
＝24×24
つまり、正方形の１辺の長さは24cmと分かります。

（２）

(1)で求めた１辺の長さ24cmを参考にすると、右上の青い紙に重ねられた右下の紙は、長い辺の長さが16cmと分かります。そうすると、見えている部分の面積が144㎠になるためには、短い辺の長さが9cmでなければならないので、これは黄の紙と分かります。
同じように、右下の黄の紙に重ねられた左下の紙は、正方形の１辺が24cmであることから、長い辺の長さが15cmとなり、見えている部分の面積が144㎠になるためには、短い辺の長さが9.6cmでなければならないので、これは白の紙と分かります。
また、残った赤い紙が左上にくるはずで、その見えている部分の面積を計算すると、
6×8＋（14.4－8）×15＝144㎠
と、こちらもうまく同じ面積になることが確かめられます。

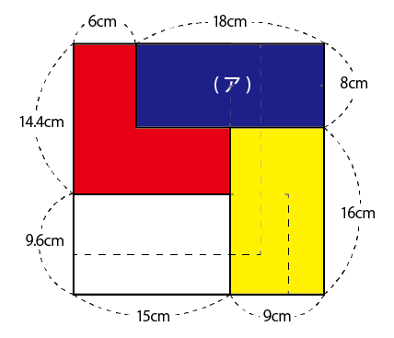
なお、上の図は、見えていない部分も点線で示してみましたが、赤い紙だけはたてと横の向きが逆でも成立します。
したがって、これらのことを総合して考えると、下から順に、「赤→白→黄→青」の順であることが分かります。

（３）

青の見えている部分の面積が105.6㎠、黄が156㎠であることが与えられていますが、青は144㎠、黄は180㎠がもともとの面積ですから、いずれも一番上の紙ではありません。
また、[図]と同じ大きさの正方形ですから、１辺の長さは24cm、面積は576㎠ですので、ここから青と黄の見えている部分の面積を引くと、残りは314.4㎠です。赤い紙全体の面積は360㎠ですから、これがすべて見えているはずはありません。したがって、一番上に重なった紙は「白」です。また、一番上にある白の紙は、すべて「見えている部分」になりますから、その面積は192㎠です。
さて、ここで、青の紙の「見えている部分の面積」が整数値でないことに注目します。白の紙の9.6cmという辺が関わらなければ面積が小数値にはならないでしょうから、白い紙によって、青の紙が隠されていることが想像できるでしょう。青の見えていない面積は144－105.6＝38.4㎠、これが白い紙の9.6cmの辺で隠されているとすれば、その長さは、38.4÷9.6＝4cmです。青の短い辺8cmのうち、4cmが白に隠されると、残りの見えている部分は4cm。これに、白の長い辺20cmを合わせるとちょうど24cmになります。

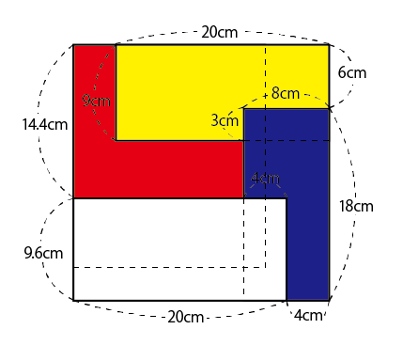
一方で、黄の紙は156㎠が見えていますが、もとの紙の面積は180㎠なので、重なって見えなくなった部分は24㎠です。これは、青の紙の短い辺8cmが3cm分だけ重なった面積なので、黄の紙の短い辺6cmから重なった3cmを引くと残りは18cm、これと青の長い辺が合わさるとちょうど24cmになります。
これらを総合して考えると、向きが異なる様々な重ね方が考えられますが、その一例が右図となります。
したがって、下から順に「赤→黄→青→白」が正解です。
ただし、このパズルをテスト中に夢中になって解き始めると、おそらく時間が足りなくなります。先ほど説明した通り、一番上が白であることはすぐに分かりますし、大きい赤が一番下であることも見当がつくでしょう。そうなると、後は青と黄の順番だけなので、勘で答えを書いても50％の確率で正解できます。また、時間内にちゃんと解けるとしても、その勘を基に青と黄の配置を描いてみて、実際に計算して探すことになると思います。

合否を分けた一題

大問［２］

（２）

2つの整数A，Bに対して，A÷Bの値を小数で表したときの小数第2020位の数を＜A÷B＞で表すことにします。例えば，2÷3＝0.666…なので，＜2÷3＞＝6です。このとき，次の問いに答えなさい。
(2) ＜N÷2020＞＝3 をみたす整数Nを1つ求めなさい。

【解法】
もちろん、一例を示せばよいだけなので、様々な数字を2020で割って試してもいずれ答えは出ますが、この方法では、よほど運がよくないと時間が掛かってしまいます。
この問題は、(1)で求めた　

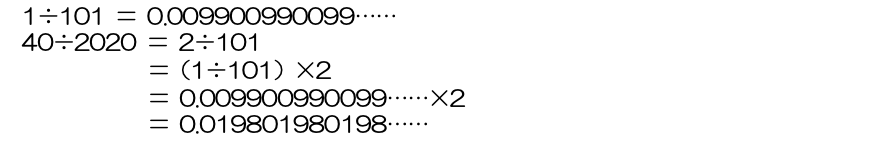
という計算がヒント（誘導）になっています。

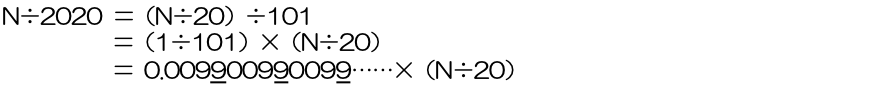
ここで、４ケタずつの周期の最後の数が小数第2020位の数字と同じになることから、99を何倍かして、一の位が3になる数を探すことになります。
99は100より1だけ小さい数ですから、「99×？」の一の位を3にするためには、100の倍数より7小さい数というのが一番簡単です。
つまり、99×7＝（100－1）×7＝100×7－1×7＝693 という考え方です。

ここから、（N÷20）＝7であればよいことが分かりますので、N＝140 が求められます。

（答え）　N＝140　（ただし一例）

駒場東邦中を目指す受験生は、正解すべき問題・時間がかかる問題・かなり難しい問題というように、
問題をまず分類し、確実に点数を積み重ねていく練習が必要となります。また、図形の移動、数に関する問題などは頻出の単元ですので、少し難しめの問題にもどんどんチャレンジしていってください。

著者：澤田重治

この記事は役にたちましたか？