算数の合否を分けた一題（2020年度）

算数の合否を分けた一題

慶應中等部入試対策・算数の合否を分けた一題（2020年度）

難易度分類

１	（１）Ａ　（２）Ａ　（３）Ａ　（４）Ａ
２	（１）Ａ　（２）Ａ　（３）Ａ　（４）Ａ
３	（１）Ｂ　（２）Ｂ　（３）Ａ　（４）Ｂ
４	（１）Ａ　（２）Ａ
５	（１）Ａ　（２）Ｂ
６	（１）Ｂ　（２）Ｃ
７	（１）Ｂ　（２）Ｃ

Ａ：慶應中等部合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難度・処理量から判断して、得点差がつかない問題

出題総評

出題傾向や問題数ともに例年通りでした。全体的に、解いたことがあり、解法の選択に迷わないものが多く、確実に解いていけたかどうかが合否を決めたと言えるでしょう。日頃の学習や過去問演習において、時間を意識して取り組み、どのくらいの時間考えて分からなければ先に進むか、といった目安を決めておくと良いでしょう。また、基本問題も疎かにせず、その式や図になる理由もきちんと考えるようにしましょう。

問題別寸評

１

計算問題２問と規則性、場合の数の小問集合です。

（１）

小数の計算問題です。安易に分数にするのではなく、小数の筆算を使って解いていきましょう。確実に正解したい問題です。

（２）

小数と分数の逆算問題です。数自体は複雑ではありませんので、こちらも確実に正解しておきましょう。

（３）

規則性・循環小数の問題です。問題自体は典型題です。最初に割り算の計算をするところをミスしないようにしましょう。

（４）

場合の数・硬貨の組み合わせの問題です。10円硬貨が5枚、100円硬貨が3枚なので、同じ金額になる払い方が複数ないパターンです。積の法則を用いて短時間で正解しておきましょう。

２

通過算・約数・旅人算・割合の小問集合です。

（１）

トンネルに入り始めてから完全に出るまでの時間を求める、通過算の典型題です。ここも確実に正解しましょう。

（２）

約数の和を求める問題です。和を求める公式を知っていれば短時間で解答できたと思いますが、公式を知らなくても、132の約数を全て書き出すことは難しくありませんので、この方法でもきちんと正解したい問題です。

（３）

池の周りを移動する旅人算の問題です。池一周の長さや二人の速さが与えられていませんので、池一周の長さを48とおいて計算しましょう。こちらも典型題でしたので確実に正解しましょう。

（４）

割合に関する問題です。問題文が少々面倒に感じるかもしれませんが、ＡとＢの比、ＢとＣの比を求め、連比を作ることができれば解くことができます。見直しもできるので確実に正解しましょう。

３

図形の問題の小問集合です。

（１）

三角形を分割し、面積比を考える問題です。
若干難度が高い問題ですが、典型題として練習してきた受験生も多いと思います。底辺一定の２つの三角形に着目していくことがポイントです。

（２）

角度の問題です。
この問題は一度解いたことがあるかないかで、正解できるかどうかが決まってしまう問題です。初見で解こうとするとどうしても角度が１つ足りず、Ｘまでたどりつくことができません。ここでは、下の図のように三角形を移動することが定石です。

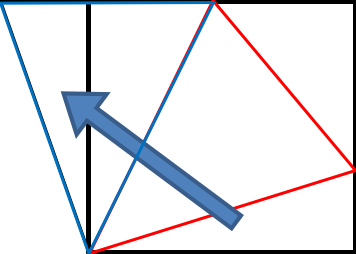
これにより、「2辺の長さと間の角が等しい」という三角形の合同条件を満たします。
よって、角度も同じ三角形となりますので、180－59×2＝62度と求められます。

（３）

直角三角形の相似形を用いた問題です。
直角をはさむ辺の長さの比が、すべて3：2となることを利用して解く問題です。（１）（２）と比べると解きやすい問題です。

（４）

回転体の表面積を求める問題です。
形が少し複雑だったため、作図をきちんとする→表面積になる面の数と形を確認する→
一つひとつの面積を丁寧に求め最後に合計を出す、といった手順を焦らず進めていく必要があります。言い換えれば、きちんと式や図を書く習慣ができていれば、正解にたどり着くことも難しくなかったと思います。

４

水そうに水を入れていく様子とグラフの問題です。
水そうの形自体そこまで複雑ではなく、また水の入れ方もシンプルな設定のため、正面から水そうを見た投影図を書き、水の体積・時間といった情報を整理できたかどうかがポイントです。普段から図を描く習慣がないと、ミスをしてしまう受験生もいたものと思われます。

（１）

容器の奥行の長さを求めて、そのあとＡＢの長さを求めましょう。比を用いて解くと
時間が短縮できます。慶應中等部の場合、答えが整数か小数か分数のどれになるかは、問題文に示されていますので、焦る必要はありません。

（２）

（１）で辺の長さや底面積が求められていれば、丁寧に計算していくだけの問題です。
確実に正解しましょう。

５

分数の数列を用いた規則性の問題です。
こちらも多くの受験生が似たような問題を解いたことがあるでしょう。規則を見つけ、確認しながら丁寧に解き進めていくことで確実に正解したい問題です。このあと作業を要する大問が続きますので、ここを短時間で解けたかがどうかも大きなポイントです。

（１）

分母、分子に関する規則はわかりやすかったでしょう。１からある整数まで足した和である三角数をどこまでおぼえていたかがポイントです。
1＋2＋…＋20＝210　を知っていれば、203番目は、1＋2＋…＋19＋13となり、
20組目の前から13番目の分数であることがわかります。
20組目の分母は21、前から13番目の分子は20－（13－1）＝8と求まりますが、きちんと問題文の数列と照らし合わせながら答えを求めることが、ミスを防ぐコツです。

（２）

６

立方体の見取り図から積み木の組み合わせを考える問題です。
斜め上から見た見取り図では、色が分からない立方体が何個か出てきます。そこの組み合わせを考えていく、場合の数の問題でした。

（１）

今見えている立方体は全部で19個あり、色の内訳は、白13個・黒6個です。
残り8個について、全部白色のときが最も軽く、全部黒色のときが最も重いことになります。ここまで分かれば、あとは計算に気をつけて答えを求めましょう。

（２）

まずは個数の合計64個、重さの合計378ｇから、つるかめ算でＡとＢの個数を求め
ます。そうするとＡ（白）が35個、Ｂ（黒）が29個と求められます。
次に、64個を使って、1辺が4㎝の立方体を作ったとき、見えている面の数で区別します。
3面見えている・・・8個
2面見えている・・・24個
1面見えている・・・24個
面が見えていない・・8個
黒く塗られている部分の面積が最も小さいのは、29個のＢを「見えている面の数が少ない
ほうから置いていく」ことになります。つまり、
面が見えていない8個のうち8個が黒
1面見えている24個のうち21個が黒　となります。
よって、最も小さい場合の黒の面積は、21㎠です。
最も大きい場合はこの逆で、
3面見えている8個のうち8個が黒
2面見えている24個のうち21個が黒　となります。
よって、最も大きい場合の黒の面積は、3×8＋2×21＝66㎠です。
つるかめ算までは気がつけても、そこからの進め方で悩んだ受験生が多かったのでは、と思われます。

７

料金の組み合わせを考える、数の性質と場合の数の複合問題です。
「シュークリーム単品」「シュークリーム5個セット」「プリン単品」「プリン6個セット」
「シュークリーム2個とプリン2個セット」の5つの買い方を組み合わせて、条件を満たす数を求めます。設問ごとに、買い方をすべて考え確かめていく解き方が良いでしょう。
こちらを本年度の「合否を分けた一題」として取り上げます。

合否を分けた一題

最後の大問ということで、解答時間に余裕があまりなかったと思われます。表などを活用し、1回の作業でミスなく解けるよう、日ごろから練習しておく必要があります。

（１）

プリンを少なくとも5個買うには、
　ア　プリン単品で5個買う
　イ　プリン6個セットを買う
　ウ　シュークリーム・プリン2個ずつセットを3セット買う
　エ　2個ずつセットを2セットとプリン単品で1個買う
の4通り考えられます。また、どの場合でもシュークリームはできるだけ5個のセットで買うほうが得します。以上のことに注意して、シュークリームが最大何個買えるかを求めましょう。
　ア　5000－220×5＝3900　3900÷800＝4あまり700
　　　700÷180＝3あまり160
　　→シュークリームは、4×5＋3＝23個買えます。

　イ　5000－1200＝3800　3800÷800＝4あまり600
　　　600÷180＝3あまり60
　　→シュークリームは、4×5＋3＝23個買えます。

　ウ　5000－650×3＝3050　3050÷800＝3あまり650
　650÷180＝3あまり110
→シュークリームは、2×3＋3×5＋3＝24個買えます。

　エ　5000－650×2－220＝3480　3480÷800＝4あまり280
　　　280÷180＝1あまり100
　　→シュークリームは、2×2＋4×5＋1＝25個買えます。

よって、買うことができる個数は最大25個です。

（２）

まずは、プリンをできるだけ多く買う場合を考えます。
①50個すべてプリンを買う場合
買い方は、ア：全て単品（1個220円）で買う
　　　　　イ：単品（1個220円）と6個セット（1200円）を組み合わせる
の2通りあります。
アの場合　220×50＝11000円
イの場合、最小で1200×8＋220×2＝10040円　となるので、
どう組み合わせてもプリン50個は買えないことになります。

②プリンを49個、シュークリームを1個買う場合
アの場合　220×49＋180×1＝10960円
イの場合　最小で1200×8＋220×1＋180×1＝10000円となり、条件を満たします。
したがって、太郎君が買ったプリンの個数は49個になります。

次に、シュークリームをできるだけ多く買う場合です。
③50個すべてシュークリームを買う場合
こちらの買い方は、ウ：全て単品（1個180円）で買う
エ：単品（1個180円）と5個セット（800円）を組み合わせる
の2通りあります。
ウの場合　180×50＝9000円
エの買い方をすると必ず、9000円よりも安くなってしまいます。
いずれにしても50個全てシュークリームを買うことはできません。

④シュークリームを49個、プリンを1個買う場合
③より、シュークリームは単品で買わないと10000円に届かないことがわかりました。
したがって、最大となるウの買い方で計算すると、
180×49＋220×1＝9040円　になります。これも10000円には届きません

⑤シュークリームを28個、プリンを2個買う場合
この個数のとき、もう1つの買い方が出てきます。
オ：プリン2個とシュークリーム2個のセットを組み合わせる
しかし、この2個ずつセットは、全て単品で買うよりも安いため、セットを組み合わせる
ことで10000円には届かなくなってしまいます。
このことから、シュークリームをなるべく多く買う場合、シュークリーム・プリンともに、
全て単品で買うことになります。
あとは、つるかめ算で求めましょう。
220×50－10000＝1000
1000÷（220－180）＝25
二郎君が買ったシュークリームの個数は25個になります。

慶應中等部を目指す受験生の方は、まず基礎の力をしっかり固め、確実に早く解けるように
なりましょう。そのうえで、解けるけど時間がかかる問題を見極め、限られた時間で最大の得点が取れるよう、問題選定の目を養っていくことが重要です。

著者：亀井章三

この記事は役にたちましたか？